题目内容
如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB，D为垂足，若AC=4，BC=3，则sin∠ACD的值为分析：先由勾股定理求出AB的长，再根据∠B+∠A=90°，∠A+∠ACD=90°可知∠B=∠ACD．运用三角函数的定义解答．
解答：解：∵Rt△ABC中，∠ACB=90°，CD⊥AB，D为垂足，AC=4，BC=3，
∴AB=
=5．
根据同角的余角相等，得∠ACD=∠B．
∴sin∠ACD=sin∠B=
=
．
∴AB=
| AC2+BC2 |
根据同角的余角相等，得∠ACD=∠B．
∴sin∠ACD=sin∠B=
| AC |
| AB |
| 4 |
| 5 |
点评：本题考查了勾股定理和锐角三角函数的定义，难度不大．
练习册系列答案
相关题目
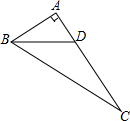如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，BD=5，则点D到BC的距离是（ ）
21、如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB，∠A=55°，则∠DCB=
22、如图所示，在Rt△ABC中，∠C=90°，∠A=30°．作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F，连接BE． 求证：EF=2DE．
如图所示，在Rt△ABC中，∠C=90°，AC=6，sinB=
如图所示，在Rt△ABC中，AD平分∠BAC，交BC于D，CH⊥AB于H，交AD于F，DE⊥AB垂足为E，求证：四边形CFED是菱形．