题目内容
5.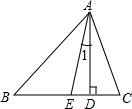 如图,△ABC中,AD是高,AE是角平分线,
如图,△ABC中,AD是高,AE是角平分线,①若∠B=50°,∠C=70°,分别求∠BAC、∠CAD和∠BAE的度数;
②若∠B=n°,∠C=m°,其中m>n,求∠1的度数.
分析 ①由三角形内角和定理求出∠BAC,由角的互余关系求出∠CAD,由角平分线的定义求出∠BAE即可;
②同①求出∠BAC、∠CAE、∠CAD,即可得出∠1的度数.
解答 解:①∵∠B=50°,∠C=70°,
∴∠BAC=180°-50°-70°=60°,
∵AD⊥BC,∠C=70°,
∴∠CAD=180°-90°-70°=20°,
∵AE是∠BAC角平分线,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=30°;
②∵∠B=n°,∠C=m°,
∴∠BAC=180°-n°-m°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CAD=90°-m°,
∵AE是∠BAC角平分线,
∴∠BAE=∠CAE=$\frac{1}{2}$∠BAC=90°-$\frac{m°}{2}$-$\frac{n°}{2}$,
∴∠1=∠CAE-∠DAC=$\frac{m°}{2}$-$\frac{n°}{2}$.
点评 本题考查了三角形内角和定理、三角形的角平分线、高;熟练掌握三角形内角和定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
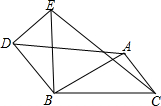 如图所示,△DBE是△ABC绕点B逆时针旋转后得到的,已知△ABC中,AB=2cm,BC=2.5cm,点A与点D的连线长为2$\sqrt{2}$cm
如图所示,△DBE是△ABC绕点B逆时针旋转后得到的,已知△ABC中,AB=2cm,BC=2.5cm,点A与点D的连线长为2$\sqrt{2}$cm 如图,∠1=∠ABC,∠2+∠D=180°,EF与CD平行吗?AB与CD平行吗?说明理由.
如图,∠1=∠ABC,∠2+∠D=180°,EF与CD平行吗?AB与CD平行吗?说明理由. 已知:如图,直线AB和CD相交于点O,OD平分∠BOF,OE⊥CD,垂足为O,∠1=40°,分别求∠2,∠3和∠EOF的度数.
已知:如图,直线AB和CD相交于点O,OD平分∠BOF,OE⊥CD,垂足为O,∠1=40°,分别求∠2,∠3和∠EOF的度数.