题目内容
 如图,在平面直角坐标系中,△ABC的顶点A(1,3),B(1,O),C(3,0).
如图,在平面直角坐标系中,△ABC的顶点A(1,3),B(1,O),C(3,0).(1)将△ABC平移得到△A1B1C1,使A点对应点A1落在x轴上,C点对应点C1落在y轴上,在图中画出△A1B1C1;
(2)将△A1B1C1绕原点逆时针旋转90°得到△A2B2C2,请直接写出A2、B2、C2的坐标.
(3)请直接写出△ACA2的面积.
考点:作图-旋转变换,作图-平移变换
专题:
分析:(1)A点对应点A1落在x轴上,C点对应点C1落在y轴上,则是把三角形向下平移4个单位长度,向左平移3个单位长度,据此即可作出三角形;
(2)把△A1B1C1的三个定点分别绕原点逆时针旋转90°,然后把对应的定点连接即可得到所求的三角形,然后写出点的坐标即可;
(3)作AD⊥x轴,延长CB交y轴于点E,根据S△ACA2=S梯形ADEC+S△ECA2-S△ADA2即可求解.
(2)把△A1B1C1的三个定点分别绕原点逆时针旋转90°,然后把对应的定点连接即可得到所求的三角形,然后写出点的坐标即可;
(3)作AD⊥x轴,延长CB交y轴于点E,根据S△ACA2=S梯形ADEC+S△ECA2-S△ADA2即可求解.
解答:解:(1)
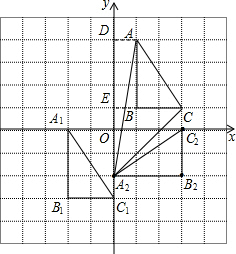
(2)出A2、B2、C2的坐标分别是:(0,-2),(3,-2),(3,0);
(3)作AD⊥x轴,延长CB交y轴于点E.
则S梯形ADEC=
(AD+CE)•DE=
(1+3)×3=6,
S△ECA2=
•EC•EA2=
×3×3=4.5,
S△ADA2=
AD•D2=
×1×6=3,
则S△ACA2=S梯形ADEC+S△ECA2-S△ADA2=6+4.5-3=7.5.

(2)出A2、B2、C2的坐标分别是:(0,-2),(3,-2),(3,0);
(3)作AD⊥x轴,延长CB交y轴于点E.
则S梯形ADEC=
| 1 |
| 2 |
| 1 |
| 2 |
S△ECA2=
| 1 |
| 2 |
| 1 |
| 2 |
S△ADA2=
| 1 |
| 2 |
| 1 |
| 2 |
则S△ACA2=S梯形ADEC+S△ECA2-S△ADA2=6+4.5-3=7.5.
点评:本题考查旋转变换作图,在找旋转中心时,要抓住“动”与“不动”,看图是关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
已知实数x,y满足|x-7|+
=0,则以x,y的值为两边长的等腰三角形的周长是( )
| y-16 |
| A、30或39 | B、30 |
| C、39 | D、以上答案均不对 |
一个正数的平方根是2a-1和a-2,则这个数是( )
| A、1 | B、4 | C、9 | D、16 |
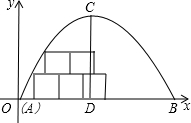 如图,某储藏室横截面呈抛物线,已知跨度AB=8米,最高点C到地面的距离CD=4米.
如图,某储藏室横截面呈抛物线,已知跨度AB=8米,最高点C到地面的距离CD=4米. 在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过点M作MN∥BC交AC于点N,以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过点M作MN∥BC交AC于点N,以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x. 如图,在△ABC和△PQD中,
如图,在△ABC和△PQD中,