题目内容
如图,在 中,
中, ,
, 是
是 的中位线,点
的中位线,点 在
在 延长上,且
延长上,且 .求证:四边形
.求证:四边形 是等腰梯形.
是等腰梯形.
 中,
中, ,
, 是
是 的中位线,点
的中位线,点 在
在 延长上,且
延长上,且 .求证:四边形
.求证:四边形 是等腰梯形.
是等腰梯形.
证明见解析
证法一: DE是
DE是 的中位线,∴DE∥AC,且
的中位线,∴DE∥AC,且 . ……………(1分)
. ……………(1分)
∴DE≠AF,∴四边形ADEF是梯形. …………………………………(2分)
 DE∥AC,∴
DE∥AC,∴ .
.
 ,∴ CF=DE,
,∴ CF=DE,
又 CE=BE,∴ ≌
≌ .∴ EF=BD, ……………………………(5分)
.∴ EF=BD, ……………………………(5分)
又 AD=BD,∴ AD=EF.所以 四边形ADEF是等腰梯形. ……………(6分)
证法二:(证明四边形ADEF是梯形,同法一)……………………………………………(2分)
连接CD. D为AB中点,∴
D为AB中点,∴ .
.

 ∥
∥ ,且
,且 =
= ,∴四边形CDEF是平行四边形. ……………(5分)
,∴四边形CDEF是平行四边形. ……………(5分)
∴CD=EF,∴AD=EF,∴四边形ADEF为等腰梯形. ……………………(6分)
三角形的中位线平行于第三边,并且等于第三边的一半;证得 ≌
≌ ,可得EF=BD,从而得到AD=EF,即四边形CDEF是等腰梯形。
,可得EF=BD,从而得到AD=EF,即四边形CDEF是等腰梯形。
 DE是
DE是 的中位线,∴DE∥AC,且
的中位线,∴DE∥AC,且 . ……………(1分)
. ……………(1分)∴DE≠AF,∴四边形ADEF是梯形. …………………………………(2分)
 DE∥AC,∴
DE∥AC,∴ .
.
 ,∴ CF=DE,
,∴ CF=DE,又 CE=BE,∴
 ≌
≌ .∴ EF=BD, ……………………………(5分)
.∴ EF=BD, ……………………………(5分)又 AD=BD,∴ AD=EF.所以 四边形ADEF是等腰梯形. ……………(6分)
证法二:(证明四边形ADEF是梯形,同法一)……………………………………………(2分)
连接CD.
 D为AB中点,∴
D为AB中点,∴ .
.
 ∥
∥ ,且
,且 =
= ,∴四边形CDEF是平行四边形. ……………(5分)
,∴四边形CDEF是平行四边形. ……………(5分)∴CD=EF,∴AD=EF,∴四边形ADEF为等腰梯形. ……………………(6分)
三角形的中位线平行于第三边,并且等于第三边的一半;证得
 ≌
≌ ,可得EF=BD,从而得到AD=EF,即四边形CDEF是等腰梯形。
,可得EF=BD,从而得到AD=EF,即四边形CDEF是等腰梯形。
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 、
、 是□
是□ 的对角线
的对角线 上的两点,
上的两点, .
.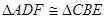 ;(2)
;(2)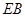 ∥
∥ .
.



 时,它是菱形
时,它是菱形 时,它是正方形
时,它是正方形 时,它是矩形
时,它是矩形 时,它是菱形
时,它是菱形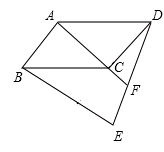
 中,
中, ,
, 平分
平分 交
交 于
于 点,在线段
点,在线段 (
( 点除外),过
点除外),过 ,分别交
,分别交 于
于 点,作
点,作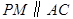 ,交
,交 于
于 点,连结
点,连结 .
. 为菱形;
为菱形; 面积的一半?
面积的一半?
 中,点
中,点 分别在边
分别在边 ,
, ,
, 上,且
上,且 ,
, .下列四个判断中,不正确的是( )
.下列四个判断中,不正确的是( )
 是平行四边形
是平行四边形 ,那么四边形
,那么四边形 平分
平分 ,那么四边形
,那么四边形 且
且 ,那么四边形
,那么四边形