题目内容
已知等腰 中,
中, ,
, 平分
平分 交
交 于
于 点,在线段
点,在线段 上任取一点
上任取一点 (
( 点除外),过
点除外),过 点作
点作 ,分别交
,分别交 于
于 点,作
点,作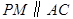 ,交
,交 于
于 点,连结
点,连结 .
.
(1)求证:四边形 为菱形;
为菱形;
(2)当 点在何处时,菱形
点在何处时,菱形 的面积为四边形
的面积为四边形 面积的一半?
面积的一半?

 中,
中, ,
, 平分
平分 交
交 于
于 点,在线段
点,在线段 上任取一点
上任取一点 (
( 点除外),过
点除外),过 点作
点作 ,分别交
,分别交 于
于 点,作
点,作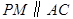 ,交
,交 于
于 点,连结
点,连结 .
.(1)求证:四边形
 为菱形;
为菱形;(2)当
 点在何处时,菱形
点在何处时,菱形 的面积为四边形
的面积为四边形 面积的一半?
面积的一半?
(1) ,
, 四边形
四边形 为平行四边形.
为平行四边形.
 平分
平分
 ,
,
 四边形
四边形 为菱形.
为菱形.
(2) 为
为 中点时,
中点时, .
.
 四边形
四边形 为菱形,
为菱形, ,
,
又
 四边形
四边形 为平行四边形.
为平行四边形.
作 于
于 ,则
,则 .
.
 ,
, 四边形
四边形 为平行四边形.
为平行四边形. 平分
平分
 ,
, 四边形
四边形 为菱形.
为菱形.(2)
 为
为 中点时,
中点时, .
. 四边形
四边形 为菱形,
为菱形, ,
,又

 四边形
四边形 为平行四边形.
为平行四边形.作
 于
于 ,则
,则 .
.(1)易证四边形 为平行四边形.利用“平行线+角平分线
为平行四边形.利用“平行线+角平分线 等腰三角形”得到EA=EP,从而证明四边形
等腰三角形”得到EA=EP,从而证明四边形 为菱形.
为菱形.
(2)根据“菱形的对角线互相垂直以及等腰三角形的三线合一”,易得EM∥BC.又 ,从而得四边形
,从而得四边形 为平行四边形.利用等高的平行四边形的面积之比等于底边的比,得到点P的位置.
为平行四边形.利用等高的平行四边形的面积之比等于底边的比,得到点P的位置.
 为平行四边形.利用“平行线+角平分线
为平行四边形.利用“平行线+角平分线 等腰三角形”得到EA=EP,从而证明四边形
等腰三角形”得到EA=EP,从而证明四边形 为菱形.
为菱形.(2)根据“菱形的对角线互相垂直以及等腰三角形的三线合一”,易得EM∥BC.又
 ,从而得四边形
,从而得四边形 为平行四边形.利用等高的平行四边形的面积之比等于底边的比,得到点P的位置.
为平行四边形.利用等高的平行四边形的面积之比等于底边的比,得到点P的位置.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, ,
, 是
是 在
在 延长上,且
延长上,且 .求证:四边形
.求证:四边形 是等腰梯形.
是等腰梯形.

 ABCD 中, AB
ABCD 中, AB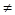 AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则
AD ,对角线 AC 与 BD 相交于点 O , OE⊥BD交 AD 于 E ,若△ABE 的周长为 12cm ,则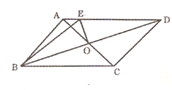
 的正方形覆盖
的正方形覆盖 的正方形网格,最多覆盖边长为
的正方形网格,最多覆盖边长为





 cm
cm cm
cm 中,
中, ,
, , 点
, 点 是
是 的中点,
的中点, ,则
,则 等于( )
等于( )




