ΧβΡΩΡΎ»ί
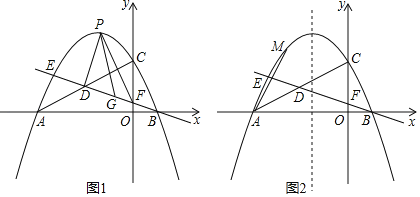
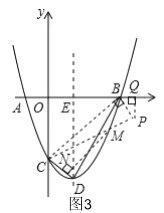
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΘΚ≈ΉΈοœΏyΘΫx2+bx+c”κx÷αΫΜ”ΎAΘ®©¹1Θ§0Θ©Θ§BΘ®3Θ§0Θ©ΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§ΒψDΈΣΕΞΒψΘ§Ν§Ϋ”BDΘ§CDΘ§≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΫΜ”κΒψEΘ°
Θ®1Θ©«σ≈ΉΈοœΏΫβΈω ΫΦΑΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©G «≈ΉΈοœΏ…œBΘ§D÷°ΦδΒΡ“ΜΒψΘ§«“SΥΡ±Ώ–ΈCDGBΘΫ4SΓςDGBΘ§«σ≥ωGΒψΉχ±ξΘΜ
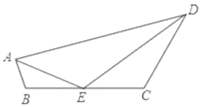
Θ®3Θ©‘Ύ≈ΉΈοœΏ…œBΘ§D÷°Φδ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ΙΐΒψMΉςMNΓΆCDΘ§ΫΜ÷±œΏCD”ΎΒψNΘ§ Ι“‘CΘ§MΘ§NΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςBDEœύΥΤΘΩ»τ¥φ‘ΎΘ§«σ≥ω¬ζΉψΧθΦΰΒΡΒψMΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΕΞΒψ
ΘΜΕΞΒψ![]()
![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§Βψ
ΘΜΘ®3Θ©¥φ‘ΎΘ§Βψ![]() Μρ
Μρ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©άϊ”Ο¥ΐΕ®œΒ ΐΖ®Ω…«σΒΟ≈ΉΈοœΏΒΡΫβΈω ΫΘ§»ΜΚσΜ·≥…ΕΞΒψ ΫΩ…ΒΟΒψDΒΡΉχ±ξΘΜ
Θ®2Θ©Ν§Ϋ”BCΘ§BGΘ§DGΘ§ Ήœ»«σ≥ω![]() Θ§»ΜΚσΗυΨίSΥΡ±Ώ–ΈCDGBΘΫ4SΓςDGBΩ…ΒΟ
Θ§»ΜΚσΗυΨίSΥΡ±Ώ–ΈCDGBΘΫ4SΓςDGBΩ…ΒΟ![]() Θ§«σ≥ω÷±œΏ
Θ§«σ≥ω÷±œΏ![]() ΒΡΫβΈω ΫΘ§…η
ΒΡΫβΈω ΫΘ§…η![]() Θ§‘ρHΘ®xΘ§2x-6Θ©Θ§ΗυΨί
Θ§‘ρHΘ®xΘ§2x-6Θ©Θ§ΗυΨί![]() ΒΟ≥ωΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σ≥ωxΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΒΟ≥ωΖΫ≥ΧΘ§ΫβΖΫ≥Χ«σ≥ωxΦ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©»γΆΦ3Θ§“‘CΘ§MΘ§NΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςBDEœύΥΤΘ§‘ρ“‘BΘ§CΘ§PΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςBDEœύΥΤΘ§‘ρ![]() Μρ
Μρ![]() Θ§«σ≥ω
Θ§«σ≥ω![]() Μρ
Μρ![]() ΘΜ»ΜΚσΖ÷
ΘΜ»ΜΚσΖ÷![]() ΚΆ
ΚΆ![]() ΝΫ÷÷«ιΩωΘ§Ζ÷±π«σ≥ω÷±œΏCPΒΡΫβΈω ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΝΫ÷÷«ιΩωΘ§Ζ÷±π«σ≥ω÷±œΏCPΒΡΫβΈω ΫΦ¥Ω…ΫβΨωΈ ΧβΘ°
ΫβΘΚΘ®1Θ©![]() ≈ΉΈοœΏ
≈ΉΈοœΏ![]() ”κ
”κ![]() ÷αΫΜ”Ύ
÷αΫΜ”Ύ![]() Θ§
Θ§![]() ΝΫΒψΘ§
ΝΫΒψΘ§
![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚ![]() ΘΜ
ΘΜ
![]() Θ§
Θ§
![]() ΕΞΒψ
ΕΞΒψ![]() ΒΡΉχ±ξΈΣ
ΒΡΉχ±ξΈΣ![]() ΘΜ
ΘΜ
Θ®2Θ©»γΆΦ2Θ§Ν§Ϋ”![]() Θ§BGΘ§DGΘ§
ȧBGȧDGȧ
‘Ύ![]() ÷–Θ§Νν
÷–Θ§Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
ΓύΒψ![]() Θ§
Θ§
Γύ“Ή«σ÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
…η÷±œΏ![]() ”κΕ‘≥Τ÷αœύΫΜ”ΎΒψ
”κΕ‘≥Τ÷αœύΫΜ”ΎΒψ![]() Θ§
Θ§
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
ΓύΒψ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ΥΡ±Ώ–Έ
ΥΡ±Ώ–Έ![]() Θ§
Θ§
![]() Θ§
Θ§
…ηΙΐΒψ![]() ”κ
”κ![]() ÷αΤΫ––ΒΡ÷±œΏΫΜBD”ΎΒψ
÷αΤΫ––ΒΡ÷±œΏΫΜBD”ΎΒψ![]() Θ§÷±œΏ
Θ§÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
‘ρ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§
Θ§
Γύ÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
…η![]() Θ§‘ρHΘ®xΘ§2x-6Θ©Θ§
Θ§‘ρHΘ®xΘ§2x-6Θ©Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
’ϊάμΒΟΘ§![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
ΓύΒψ![]() ΘΜ
ΘΜ
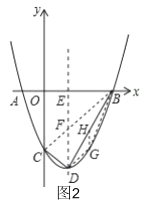
Θ®3Θ©¥φ‘ΎΘ§
”…Ι¥Ι…Ε®άμΒΟΘ§![]() Θ§
Θ§
»γΆΦ3Θ§ΙΐΒψ![]() Ής
Ής![]() ΫΜ
ΫΜ![]() ΒΡ―”≥ΛœΏ”Ύ
ΒΡ―”≥ΛœΏ”Ύ![]() Θ§
Θ§
![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
![]() Θ§
Θ§![]() ”κ
”κ![]() ÷αΒΡΦ–Ϋ«ΕΦ «
÷αΒΡΦ–Ϋ«ΕΦ «![]() Θ§
Θ§
![]() Θ§
Θ§
”÷![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() “‘
“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ![]() œύΥΤΘ§
œύΥΤΘ§
![]() “‘
“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ![]() œύΥΤΘ§
œύΥΤΘ§
![]() Μρ
Μρ![]() Θ§Φ¥
Θ§Φ¥![]() Μρ
Μρ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Μρ
Μρ![]() Θ§
Θ§
ΙΐΒψ![]() Ής
Ής![]() ÷α”Ύ
÷α”Ύ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
ΔΌΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύΒψ![]() Θ§
Θ§
…η÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
‘ρ Θ§ΫβΒΟ
Θ§ΫβΒΟ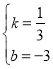 Θ§
Θ§
Γύ÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
ΝΣΝΔ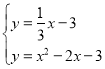 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ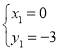 Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§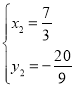 Θ§
Θ§
ΓύΒψ![]() ΘΜ
ΘΜ
ΔΎΒ±![]() ±Θ§
±Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύΒψ![]() Θ§
Θ§
…η÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
‘ρ![]() Θ§ΫβΒΟ
Θ§ΫβΒΟ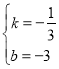 Θ§
Θ§
Γύ÷±œΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
ΝΣΝΔ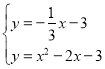 Θ§ΫβΒΟ
Θ§ΫβΒΟ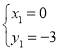 Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§ Θ§
Θ§
![]() Βψ
Βψ![]() Θ§
Θ§
Ήέ…œΥυ ωΘ§¥φ‘ΎΒψ![]() Μρ
Μρ![]() Θ§ Ι“‘
Θ§ Ι“‘![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ
ΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κ![]() œύΥΤΘ°
œύΥΤΘ°

 œΑΧβΨΪ―ΓœΒΝ–¥πΑΗ
œΑΧβΨΪ―ΓœΒΝ–¥πΑΗ