题目内容
 如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=
如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=| 1 |
| 4 |
| 5 |
考点:切线的性质,矩形的性质
专题:几何图形问题,压轴题
分析:过点G作GN⊥AB,垂足为N,可得EN=NF,由EG:EF=
:2,得:EG:EN=
:1,依据勾股定理即可求得AB的长度.
| 5 |
| 5 |
解答: 解:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,
解:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,
如图,过点G作GN⊥AB,垂足为N,
∴EN=NF,
又∵EG:EF=
:2,
∴EG:EN=
:1,
又∵GN=AD=8,
∴设EN=x,则GE=
x,根据勾股定理得:
(
x)2-x2=64,解得:x=4,GE=4
,
设⊙O的半径为r,由OE2=EN2+ON2
得:r2=16+(8-r)2,
∴r=5.∴OK=NB=5,
∴EB=9,
又AE=
AB,
∴AB=12.
同理,当边AD所在的直线与⊙O相切时,AB=4.
故答案为:12或4.
 解:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,
解:边AB所在的直线不会与⊙O相切;边BC所在的直线与⊙O相切时,如图,过点G作GN⊥AB,垂足为N,
∴EN=NF,
又∵EG:EF=
| 5 |
∴EG:EN=
| 5 |
又∵GN=AD=8,
∴设EN=x,则GE=
| 5 |
(
| 5 |
| 5 |
设⊙O的半径为r,由OE2=EN2+ON2

得:r2=16+(8-r)2,
∴r=5.∴OK=NB=5,
∴EB=9,
又AE=
| 1 |
| 4 |
∴AB=12.
同理,当边AD所在的直线与⊙O相切时,AB=4.
故答案为:12或4.
点评:本题考查了切线的性质以及勾股定理和垂径定理的综合应用,解答本题的关键在于做好辅助线,利用勾股定理求出对应圆的半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
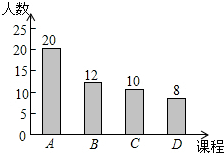 某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有
某学校计划开设A、B、C、D四门校本课程供全体学生选修,规定每人必须并且只能选修其中一门,为了了解各部门课程的选修人数.现从全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图所示的条形统计图.已知该校全体学生人数为1200名,由此可以估计选修C课程的学生有