题目内容
 如图,?ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.
如图,?ABCD在平面直角坐标系中,AD=6,若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB.(1)求AB的长;
(2)求CD的所在直线的函数关系式;
(3)若动点P从点B出发,以每秒1个单位长度的速度沿B→A方向运动,过P作x轴的垂线交x轴于点E,若S△PBE=
| 1 |
| 3 |
考点:一次函数综合题
专题:
分析:(1)首先解方程求得OA和OB的长,然后利用勾股定理求得AB的长即可;
(2)首先求得点A和点B的坐标,然后平移得到点C和点D的坐标,利用待定系数法求得直线CD的解析式即可;
(3)根据PE∥AO得到△BPE∽△BAO,利用S△PBE=
S△ABO得到相似比为
=
,从而列式
=
=
求得BE=
,PE=
,然后求得EO=BO-BE=3-
后即可求得点P的坐标.
(2)首先求得点A和点B的坐标,然后平移得到点C和点D的坐标,利用待定系数法求得直线CD的解析式即可;
(3)根据PE∥AO得到△BPE∽△BAO,利用S△PBE=
| 1 |
| 3 |
|
| ||
| 3 |
| BE |
| BO |
| PE |
| AO |
| ||
| 3 |
| 3 |
4
| ||
| 3 |
| 3 |
解答:解:(1)方程x2-7x+12=0可因式分解为(x-3)(x-4)=0,
解得:x=3或x=4,
∵OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,
∴OA=4,OB=3,
∴AB=
=5;
(2)∵OA=4,OB=3,
∴A(0,4),B(-3,0),
∵AD=BC=6,
∴C(3,0),D(6,4),
设直线CD的解析式为y=kx+b,
∴
解得:k=
,b=-4,
∴直线CD的解析式为y=
x-4;
(3)∵PE⊥x轴,
∴PE∥AO,
∴△BPE∽△BAO,
∵S△PBE=
S△ABO,
∴相似比为
=
,
∴
=
=
,
即:
=
=
,
∴BE=
,PE=
,
∴EO=BO-BE=3-
∴点P的坐标为(
-3,
);
解得:x=3或x=4,
∵OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根,且OA>OB,
∴OA=4,OB=3,
∴AB=
| OA2+OB2 |
(2)∵OA=4,OB=3,
∴A(0,4),B(-3,0),
∵AD=BC=6,
∴C(3,0),D(6,4),
设直线CD的解析式为y=kx+b,
∴
|
解得:k=
| 4 |
| 3 |
∴直线CD的解析式为y=
| 4 |
| 3 |
(3)∵PE⊥x轴,
∴PE∥AO,
∴△BPE∽△BAO,
∵S△PBE=
| 1 |
| 3 |
∴相似比为
|
| ||
| 3 |
∴
| BE |
| BO |
| PE |
| AO |
| ||
| 3 |
即:
| BE |
| 3 |
| PE |
| 4 |
| ||
| 3 |
∴BE=
| 3 |
4
| ||
| 3 |
∴EO=BO-BE=3-
| 3 |
∴点P的坐标为(
| 3 |
4
| ||
| 3 |
点评:本题考查了一次函数的综合知识,题目中多次进行了点的坐标和线段的长的转化,这是解决本题的关键,难度中等偏上.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知△ABC在平面直角坐标系中位置如图.
已知△ABC在平面直角坐标系中位置如图.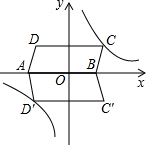 平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y=
平行四边形ABCD在平面直角坐标系中的位置如图所示,其中A(-6,0),B(4,0),C(5,3),反比例函数y= 如图,△ABC中,∠BAC=120°,AB=
如图,△ABC中,∠BAC=120°,AB= 如图,点E、F分别是?ABCD的边BC、AD上的点,且CE=AF.
如图,点E、F分别是?ABCD的边BC、AD上的点,且CE=AF. 如图坡度:AB的坡度iAB=
如图坡度:AB的坡度iAB=