题目内容
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
| 月均用水量(单位:t) | 频数 |
|
|
| 2 | 4% |
|
| 12 | 24% |
|
| ||
|
| 10 | 20% |
|
| 12% | |
|
| 3 | 6% |
|
| 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在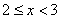 ,
,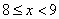 这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
解:(1)∵月均用水量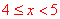 所占百分比为
所占百分比为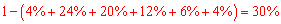 ;
;
月均用水量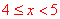 的频数为
的频数为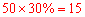 ;月均用水量
;月均用水量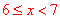 的频数为
的频数为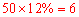 ,
,
∴补全频数分布表和频数分布直方图如下:
| 月均用水量(单位:t) | 频数 |
|
|
| 2 | 4% |
|
| 12 | 24% |
|
| 15 | 30% |
|
| 10 | 20% |
|
| 6 | 12% |
|
| 3 | 6% |
|
| 2 | 4% |
(2)∵样本中家庭月均用水量“大于或等于4t且小于7t”占62%,
∴估计总体中的中等用水量家庭大约有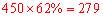 (户).
(户).
(3)设月均用水量在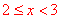 范围内的样本家庭为
范围内的样本家庭为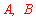 ,月均用水量在
,月均用水量在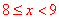 范围内的样本家庭为
范围内的样本家庭为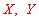 ,
,
∵从月均用水量在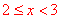 ,
,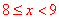 这两个范围内的样本家庭中任意抽取2个,共有6种等可能结果:
这两个范围内的样本家庭中任意抽取2个,共有6种等可能结果: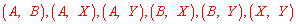 ,抽取出的2个家庭来自不同范围的有4种情况:
,抽取出的2个家庭来自不同范围的有4种情况: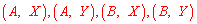 ,
,
∴抽取出的2个家庭来自不同范围的概率为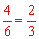 .为
.为
【考点】频数分布表和频数分布直方图;频数、频率和总量的关系;用样本估计总体;概率.
【分析】(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量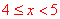 所占百分比和频数,月均用水量
所占百分比和频数,月均用水量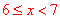 的频数,从而补全频数分布表和频数分布直方图.
的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
(3)根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.

 期末集结号系列答案
期末集结号系列答案问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成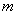 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究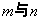 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当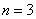 时,
时,
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当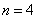 时,
时,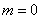
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当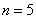 时,
时,
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当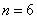 时,
时,
综上所述,可得表①
|
| 3 | 4 | 5 | 6 |
|
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2) 分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
|
| 7 | 8 | 9 | 10 |
|
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用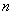 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设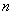 分别等于
分别等于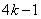 、
、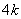 、
、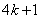 、
、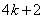 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
 百分比
百分比




 百分比
百分比 得的利润最大?获得的最大利润是多少元?
得的利润最大?获得的最大利润是多少元?  =
=

 、
、 是一元二次方程
是一元二次方程 的两实数根,则
的两实数根,则 的值为 .
的值为 .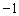 ,0),B(4,0),C(2,
,0),B(4,0),C(2,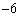 )三点.
)三点.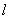 ,点
,点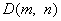
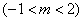 是图象M上一动点,当△ACD的面积为
是图象M上一动点,当△ACD的面积为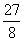 时,点D关于
时,点D关于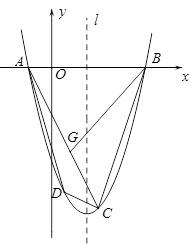
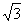 ,BD=4,则菱形ABCD的周长为( ).
,BD=4,则菱形ABCD的周长为( ). C.
C.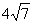 D.28
D.28 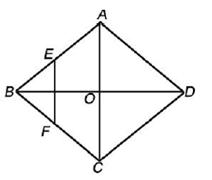
 ,求
,求 的值.
的值.