题目内容
(8分)如图,△ABC中,∠C=90°,AC=8cm,BC=4cm,一动点P从C出发沿着CB方向以1cm/S的速度运动,另一动点Q从A出发沿着AC方向以2cm/S的速度运动,P,Q两点同时出发,运动时间为t(s).

(1)当t为几秒时,△PCQ的面积是△ABC面积的  ?
?
(2)△PCQ的面积能否为△ABC面积的一半?若能,求出t的值;若不能,说明理由.
(1)t=2;(2)△PCQ的面积不可能是△ABC面积的一半,理由详见解析
【解析】
试题分析:(1)根据三角形的面积公式可以求出时间t;
(2)由等量关系S△PCQ= S△ABC列方程求出t的值,但方程无解.
S△ABC列方程求出t的值,但方程无解.
试题解析:(1)∵S△PCQ= t(8﹣2t),S△ABC=
t(8﹣2t),S△ABC= ×4×8=16,
×4×8=16,
∴ t(8﹣2t)=16×
t(8﹣2t)=16× ,
,
整理得t2﹣4t+4=0,
解得t=2.
答:当t=2s时△PCQ的面积为△ABC面积的 ;
;
(2)当S△PCQ= S△ABC时,
S△ABC时, t(8﹣2t)=16×
t(8﹣2t)=16× ,
,
整理得t2﹣4t+8=0,
△=(﹣4)2﹣4×1×8=﹣16<0,
∴此方程没有实数根,
∴△PCQ的面积不可能是△ABC面积的一半.
考点:1.一元二次方程的应用;2.三角形的面积.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目


 是方程
是方程 的两个实数根,则
的两个实数根,则 的值为 .
的值为 .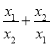 的值为( )
的值为( )

 ,并且图象过A(0,-4)和B(4,0),
,并且图象过A(0,-4)和B(4,0),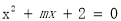 的一个解,则m的值是 ( ).
的一个解,则m的值是 ( ).