题目内容
20.函数y=$\frac{\sqrt{4-x}}{2}$中,自变量x的取值范围是x≤4.分析 根据被开方数是非负数,可得答案.
解答 解:由y=$\frac{\sqrt{4-x}}{2}$中,得
4-x≥0,
解得x≤4,
故答案为:≤4.
点评 本体考察了自变量的取值范围,函数自变量的范围一般从三个方面考虑:当函数表达式是整式时,自变量可取全体实数;当函数表达式是分式时,考虑分式的分母不能为0;当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
8.若|a|=-a,则a是( )
| A. | 非负数 | B. | 负数 | C. | 正数 | D. | 非正数 |
15.已知y=(m+1)${x}^{{m}^{2}}$,如果y是x的正比例函数,则m的值为( )
| A. | 1 | B. | -1 | C. | 1,-1 | D. | 0 |
12.下列运用等式的性质变形错误的是( )
| A. | 若a=b,则a+1=b+1 | B. | 若-3x=-3y,则x=-y | ||
| C. | 若n-2=m-2,则m-n=0 | D. | 若$\frac{a}{2}$=$\frac{b}{2}$,则a=b |
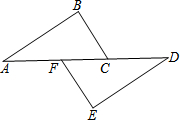 已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.