题目内容
2. 如图,将正方形ABCG和正方形CDEF按图中虚线剪拼成一个正方形AHEP,若这个新正方形AHEP的面积为13,正方形CDEF的边长为2,则正方形ABCG的边长为( )
如图,将正方形ABCG和正方形CDEF按图中虚线剪拼成一个正方形AHEP,若这个新正方形AHEP的面积为13,正方形CDEF的边长为2,则正方形ABCG的边长为( )| A. | 3 | B. | $2\sqrt{3}$ | C. | $\sqrt{11}$ | D. | $\sqrt{15}$ |
分析 根据图形的剪拼可得正方形ABCG的面积=正方形AHEP的面积-正方形CDEF的面积,根据正方形的面积公式可求正方形ABCG的面积,再根据算术平方根的定义求解即可.
解答 解:正方形ABCG的面积为:
13-2×2
=13-4
=9
正方形ABCG的边长为$\sqrt{9}$=3.
故选:A.
点评 此题考查了图形的剪拼,算术平方根,解题的关键是理解正方形ABCG的面积=正方形AHEP的面积-正方形CDEF的面积.

练习册系列答案
相关题目
12.二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
根据以上信息,某同学得到以下结论:①抛物线的开口向上;②当x>-2时,y随x的增大而增大;③二次函数的最小值是-2;④抛物线的对称轴是x=-$\frac{5}{2}$,其中正确的有( )
| x | … | -5 | -4 | -3 | -2 | -1 | 0 | … |
| y | … | 4 | 0 | -2 | -2 | 0 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
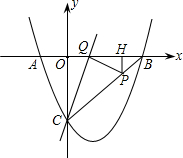 如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.
如图,已知抛物线y=$\frac{3}{4}{x}^{2}$+bx+c与轴交于A、B两点,与y轴交于C点,A的坐标为(-1,0),过点C的直线y=$\frac{3}{4t}$x-3与x轴交于点Q,点P是线段BC上的动点,过P作PH⊥OB于点H.若PB=5t,且0<t<1.