题目内容
如图,在平面直角坐标系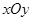 中,等边
中,等边 中,BC∥
中,BC∥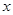 轴,且BC=
轴,且BC= ,顶点A在抛物线
,顶点A在抛物线 上运动.
上运动.

(1)当顶点A运动至与原点重合时,顶点C是否在该抛物线上?
(2) 在运动过程中有可能被
在运动过程中有可能被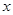 轴分成两部分,当上下两部分的面积之比为1:8(即
轴分成两部分,当上下两部分的面积之比为1:8(即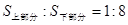 )时,求顶点A的坐标;
)时,求顶点A的坐标;
(3) 在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
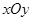 中,等边
中,等边 中,BC∥
中,BC∥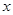 轴,且BC=
轴,且BC= ,顶点A在抛物线
,顶点A在抛物线 上运动.
上运动.
(1)当顶点A运动至与原点重合时,顶点C是否在该抛物线上?
(2)
 在运动过程中有可能被
在运动过程中有可能被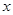 轴分成两部分,当上下两部分的面积之比为1:8(即
轴分成两部分,当上下两部分的面积之比为1:8(即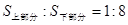 )时,求顶点A的坐标;
)时,求顶点A的坐标;(3)
 在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.
在运动过程中,当顶点B落在坐标轴上时,直接写出顶点C的坐标.(1)在;(2) 或
或 ;(3)
;(3) 、
、 、
、
 或
或 ;(3)
;(3) 、
、 、
、
试题分析:(1)当顶点A运动至与原点重合时,设BC与y轴交于点D,由BC∥x轴,BC=AC=
 ,可得
,可得 ,
, ,即可得到C点的坐标,再代入抛物线解析式即可作出判断;
,即可得到C点的坐标,再代入抛物线解析式即可作出判断;(2)过点A作
 于点D,设点A的坐标为(
于点D,设点A的坐标为(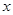 ,
, ).由
).由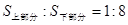 根据相似三角形的性质可得
根据相似三角形的性质可得 ,再根据等边三角形的性质可求得
,再根据等边三角形的性质可求得 的长,即可求得结果;
的长,即可求得结果;(3)根据函数图象上的点的坐标的特征结合二次函数的性质求解即可.
(1)当顶点A运动至与原点重合时,设BC与y轴交于点D
∵BC∥x轴,BC=AC=
 ,
,∴
 ,
, .
.∴C点的坐标为
 .
.∵当
 时,
时, .
.∴当顶点A运动至与原点重合时,顶点C在抛物线上;
(2)过点A作
 于点D,
于点D,
设点A的坐标为(
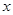 ,
, ).
).∵
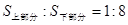 ,
,∴

∵等边
 的边长为
的边长为 ,
,∴
 .
.∴
 .
.∴
 ,解得
,解得
 .
.∴顶点A的坐标为
 或
或 ;
;(3)当顶点B落在坐标轴上时,顶点C的坐标为
 、
、 、
、 .
.点评:此类问题是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
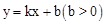 与抛物线
与抛物线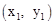 相交于A
相交于A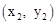 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且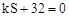 。
。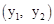 在反比例函数
在反比例函数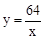 的图象上;
的图象上;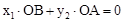 。
。

 的顶点为H,与
的顶点为H,与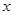 轴交于A、B两点(B点在A点右侧),点H、B关于直线:
轴交于A、B两点(B点在A点右侧),点H、B关于直线: 对称,过点B作直线BK∥AH交直线于K点.
对称,过点B作直线BK∥AH交直线于K点. 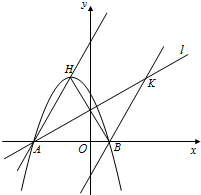
 上运动,当⊙P与
上运动,当⊙P与 轴相切时,
轴相切时,
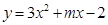 .
. 
 为任何实数,抛物线与x轴总有两个交点;
为任何实数,抛物线与x轴总有两个交点;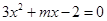 的两个有理数根都在
的两个有理数根都在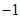 与
与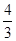 之间(不包括-1、
之间(不包括-1、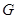 ,再将图象
,再将图象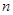 个单位,若图象
个单位,若图象 的图像与
的图像与 轴交于A、B两点,与
轴交于A、B两点,与 轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是( )
轴交于点C,连接AC,点P是抛物线上的一个动点,记△APC的面积为S,当S=2时,相应的点P的个数是( )