题目内容
11.从5名同学中任选3名,分别担任班长、团支部书记和学习委员,求:(1)甲恰好被选上,并且担任班长的概率?
(2)甲、乙两人均被选上,并且甲任班长,乙任团支部书记的概率?
分析 (1)先求出5名同学中任选3名,分别担任班长、团支部书记和学习委员的基本事件总数,再求出甲恰好被选上,并且担任班长,包含的基本事件个数,由此能求出恰好被选上,并且担任班长的概率.
(2)先求出5名同学中任选3名,分别担任班长、团支部书记和学习委员的基本事件总数,再求出甲、乙两人均被选上,并且甲任班长,乙任团支部书记,包含的基本事件个数,由此能求出甲、乙两人均被选上,并且甲任班长,乙任团支部书记的概率.
解答 解:(1)5名同学中任选3名,分别担任班长、团支部书记和学习委员,
基本事件总数n=${A}_{5}^{3}$=60,
甲恰好被选上,并且担任班长,包含的基本事件个数m1=${A}_{4}^{2}$=12,
∴甲恰好被选上,并且担任班长的概率p1=$\frac{{m}_{1}}{n}$=$\frac{12}{60}$=$\frac{1}{5}$.
(2)5名同学中任选3名,分别担任班长、团支部书记和学习委员,
基本事件总数n=${A}_{5}^{3}$=60,
甲、乙两人均被选上,并且甲任班长,乙任团支部书记,包含的基本事件个数m2=${C}_{3}^{1}$=3,
∴甲、乙两人均被选上,并且甲任班长,乙任团支部书记的概率P2=$\frac{{m}_{2}}{n}$=$\frac{3}{60}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.单项式-$\frac{3{a}^{2}{b}^{4}}{5}$的系数和次数分别是( )
| A. | $\frac{3}{5}$和6 | B. | -$\frac{3}{5}$和6 | C. | -3和6 | D. | -$\frac{1}{5}$和6 |
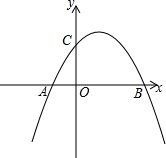 如图:已知二次函数y=-x2+bx+c图象分别交x轴于A(-$\frac{1}{2}$,0)、B($\sqrt{5}$,0)两点,交y轴于点C,过B、C两点作直线BC.
如图:已知二次函数y=-x2+bx+c图象分别交x轴于A(-$\frac{1}{2}$,0)、B($\sqrt{5}$,0)两点,交y轴于点C,过B、C两点作直线BC. 如图,Rt△ABC中,∠ACB=90°,分别以AB、BC、CA为直径向外作半圆,面积分别为S1、S2、S3三者的数量关系,并说明理由.
如图,Rt△ABC中,∠ACB=90°,分别以AB、BC、CA为直径向外作半圆,面积分别为S1、S2、S3三者的数量关系,并说明理由.