题目内容
【题目】甲乙两人准备在一段长为1200m的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s和6m/s,起跑前乙在起点,甲在乙前面100m处,两人同时起跑.
(1)两人出发后多长时间乙追上甲?
(2)求从起跑至其中一人先到达终点的过程中,甲、乙两人之间的距离y(m)与时间t(s)的函数关系,并画出y(m)与时间t(s)的图象.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ,画图见解析.
,画图见解析.
【解析】
(1)根据题意列式计算即可解答;
(2)甲在乙前面,而乙的速度大于甲,则此过程为乙先追上甲后再超过甲,全程时间为乙跑的时间,算出相遇时间,画出图象.
解:(1)100÷(6﹣4)=50s.
故两人出发后50s乙追上甲;
(2)当t≤50时,
![]() ,
,
∴![]()
当50<t≤200时,
![]()
∴![]()
全程乙跑完后计时结束:t总=![]() s,
s,
则计时结束后甲乙的距离:s=(6﹣4)×(200﹣50)=300m,
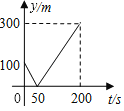
故甲、乙两之间的距离y(m)与时间t(s)的函数图象如图所示:

练习册系列答案
相关题目