Question

【题目】如图，在平面直角坐标系中，线段AB的端点坐标为A（﹣1，2），B（3，1），若直线y＝kx﹣2与线段AB有交点，则k的值可能是（　　）

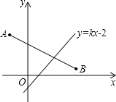
A. ﹣3B. ﹣2C. ﹣1D. 2

Answer 1

【答案】D

【解析】

先求出直线y=kx-2与y轴的交点C的坐标，再利用待定系数法求出直线AC、BC的解析式，然后根据直线与线段AB有交点，则k值小于AC的k值，或大于BC的k值，然后根据此范围进行选择即可．

解：令x＝0，则y＝0k﹣2＝﹣2，

所以直线y＝kx﹣2与y轴的交点坐标为（0，﹣2），

设直线AC的解析式为y＝mx+n，

则，

解得．

所以直线AC的解析式为y＝﹣4x﹣2，

设直线BC的解析式为y＝ex+f，

则，

解得．

所以直线BC的解析式为y＝x﹣2，

若直线y＝kx﹣2与线段AB有交点，则k的取值范围是k≤﹣4或k≥1，

纵观各选项，只有D选项符号．

故选：D．