Question

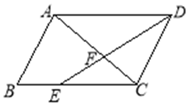
【题目】如图，在平行四边形ABCD中，点E在BC边上，且CE︰BC＝2︰3，AC与DE相交于点F，若S△EFC=8，则S△CFD＝________．

Answer 1

【答案】12

【解析】由于四边形ABCD是平行四边形，所以得到BC∥AD、BC=AD，而CE：BC=2：3，由此即可得到△AFD∽△CFE，它们的相似比为3：2，利用相似三角形的性质得到FD：FE=3：2，即S△CDF：S△EFC=3：2，由此即可求解．

∵四边形ABCD是平行四边形，∴BC∥AD、BC=AD，而CE：BC=2：3，∴△AFD∽△CFE，且它们的相似比为3：2，∴FD：FE=3：2，∴S△CDF：S△EFC=3：2，而S△EFC=8，∴S△DFC=12．

故答案为：12．