题目内容
已知一元二次方程x2+2x+m=0的两个实根为x1、x2，且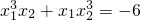
，求m的值．
解：∵一元二次方程x2+2x+m=0的两个实根为x1、x2，
∴△=4-4m≥0，即m≤1．
根据韦达定理，知
x1+x2=-2，x1•x2=m，
∴
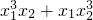=x1•x2[（x1+x2）2-2x1•x2]=m（4-2m）=6，即（m-3）（m+1）=0，
解得，m=3（不合题意，舍去）或m=-1．
故m的值是-1．
分析：首先根据根与系数的关系求得x1+x2=-2，x1•x2=m；然后将其代入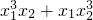=x1•x2[（x1+x2）2-4x1•x2]=6，通过解方程即可求得m的值．
点评：本题考查了根与系数的关系．注意，关于x是一元二次方程x2+2x+m=0有两个实根时，必须通过根的判别式确定m的取值范围．
∴△=4-4m≥0，即m≤1．
根据韦达定理，知
x1+x2=-2，x1•x2=m，
∴
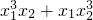=x1•x2[（x1+x2）2-2x1•x2]=m（4-2m）=6，即（m-3）（m+1）=0，解得，m=3（不合题意，舍去）或m=-1．
故m的值是-1．
分析：首先根据根与系数的关系求得x1+x2=-2，x1•x2=m；然后将其代入
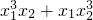=x1•x2[（x1+x2）2-4x1•x2]=6，通过解方程即可求得m的值．点评：本题考查了根与系数的关系．注意，关于x是一元二次方程x2+2x+m=0有两个实根时，必须通过根的判别式确定m的取值范围．
练习册系列答案
相关题目