题目内容
观察下列各式,找规律:
①32﹣12=4×2;
②42﹣22=4×3;
③52﹣32=4×4;
④62﹣42=4×5,
第n个等式是 .(n是正整数)
(n+2)2﹣n2=4(n+1) .(n是正整数)
【考点】规律型:数字的变化类.
【专题】规律型.
【分析】观察不难发现,一个数与比它小2的两个数的平方差等于比这个数小1的数的4倍.
【解答】解:∵①32﹣12=4×2;
②42﹣22=4×3;
③52﹣32=4×4;
④62﹣42=4×5,
…,
∴第n个等式为(n+2)2﹣n2=4(n+1).
故答案为:(n+2)2﹣n2=4(n+1).
【点评】本题是对数字变化规律的考查,比较简单,难点在于要注意底数与等式序号的关系.

练习册系列答案
相关题目
 .
.
 ,则扇形的圆心角为 .
,则扇形的圆心角为 . ,3y=
,3y= ,求9x﹣y的值.
,求9x﹣y的值.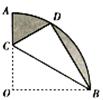
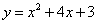 交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0)。
交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0)。 ,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;
,与A、B、C三点构成一个平行四边形?若存在,请写出点P的坐标;若不存在,请说明理由;