Question

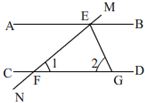20、如图，直线MN分别交直线AB，CD于点E，F，EG平分∠BEF，若∠1=50°，∠2=65°，
（1）求证：AB∥CD；
（2）在（1）的条件下，求∠AEM的度数．

Answer 1

分析：（1）根据三角形的内角和定理能求出∠FEG的度数，由EG平分∠BEF，求出∠BEF的度数，计算出∠BEF+∠1=180°，根据平行线的判定定理即可得到答案；
（2）根据对顶角相等即可求出答案．

解答：（1）证明：∵∠1+∠2+∠FEG=180°，
∵∠1=50°，∠2=65°，
∴∠FEG=65°，
∵EG平分∠BEF，
∴∠BEF=2∠FEG=130°，
∴∠BEF+∠1=180°，
∴AB∥CD．
（2）∵∠AEM=∠BEF，
∵∠BEF=130°，
∴∠AEM=130°，
答：∠AEM的度数是130°．

点评：本题主要考查了平行线的性质，三角形的内角和定理，角平分线的性质，对顶角的性质等知识点，解此题的关键是求出∠BEF+∠1=180°，题型较好．