题目内容
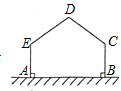 用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为
用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为
- A.12
 m2
m2 - B.12m2
- C.24
 m2
m2 - D.没有最大值
A
分析:已知AE⊥AB,BC⊥AB,∠C=∠D=∠E.就可以求出五边形的各个角的度数,连接EC,则△DEC是等腰三角形.四边形EABC为矩形,在△DEC中若作DF⊥EC,依据三线合一定理以及三角函数就可以用DE表示出EC的长,再根据总长是12m,AE就可以用x表示出来,因而五边形的面积写成△DEC于矩形EABC的和的问题,就可以把面积表示成x的函数,转化为求二次函数的最值问题.
解答: 解:连接EC,作DF⊥EC,垂足为F
解:连接EC,作DF⊥EC,垂足为F
∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°,
∵DE=CD
∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,
∴四边形EABC为矩形,
∴DE=xm,
∴AE=6-x,DF= x,EC=
x,EC= x,
x,
s=- x2+6
x2+6 x(0<x<6).
x(0<x<6).
∴当x=4m时,S最大=12 m2.
m2.
故选A.
点评:本题求最值问题解决的基本思路是转化为函数问题,转化为依据函数问题求最值的问题.
分析:已知AE⊥AB,BC⊥AB,∠C=∠D=∠E.就可以求出五边形的各个角的度数,连接EC,则△DEC是等腰三角形.四边形EABC为矩形,在△DEC中若作DF⊥EC,依据三线合一定理以及三角函数就可以用DE表示出EC的长,再根据总长是12m,AE就可以用x表示出来,因而五边形的面积写成△DEC于矩形EABC的和的问题,就可以把面积表示成x的函数,转化为求二次函数的最值问题.
解答:
 解:连接EC,作DF⊥EC,垂足为F
解:连接EC,作DF⊥EC,垂足为F∵∠DCB=∠CDE=∠DEA,∠EAB=∠CBA=90°,
∴∠DCB=∠CDE=∠DEA=120°,
∵DE=CD
∴∠DEC=∠DCE=30°,
∴∠CEA=∠ECB=90°,
∴四边形EABC为矩形,
∴DE=xm,
∴AE=6-x,DF=
 x,EC=
x,EC= x,
x,s=-
 x2+6
x2+6 x(0<x<6).
x(0<x<6).∴当x=4m时,S最大=12
 m2.
m2.故选A.
点评:本题求最值问题解决的基本思路是转化为函数问题,转化为依据函数问题求最值的问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
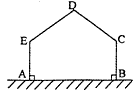
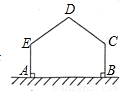
 用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为( )
用长为12m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=xm,五边形ABCDE的面积为S m2.则S的最大值为( )A、12
| ||
| B、12m2 | ||
C、24
| ||
| D、没有最大值 |
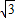 m2
m2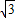 m2
m2