题目内容
22、有长为24m的篱笆,打算利用一面墙围城一个花圃
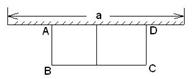
(1)要使花圃成为长方形(如图1),并且面积为40m2,问这个长方形相邻两边的长各是多少?
(2)如果墙的可用长度为12m,打算用这24m长的篱笆围成中间有两条隔断的长方形花圃(如图2),这三个小长方形花圃的总面积能够达到32m2吗?若能,给出你的方案?若不能,请说明理由.
(1)要使花圃成为长方形(如图1),并且面积为40m2,问这个长方形相邻两边的长各是多少?
(2)如果墙的可用长度为12m,打算用这24m长的篱笆围成中间有两条隔断的长方形花圃(如图2),这三个小长方形花圃的总面积能够达到32m2吗?若能,给出你的方案?若不能,请说明理由.

分析:(1)可设垂直于墙的长方形的边长为未知数,等量关系为:垂直于墙的长方形的边长×(24-2垂直于墙的长方形的边长)=40,把相关数值代入求得合适的解即可;
(2)等量关系为:垂直于墙的长方形的边长×(24-4垂直于墙的长方形的边长)=32,把相关数值代入求得合适的解即可.
(2)等量关系为:垂直于墙的长方形的边长×(24-4垂直于墙的长方形的边长)=32,把相关数值代入求得合适的解即可.
解答:解:(1)设垂直于墙的长方形的边长为xm.
x(24-2x)=40,
解得x1=2,x2=10,
当x=2时,24-2x=20;
当x=10时,24-2x=4;
答:这个长方形相邻两边的长分别为2m,20m;或10m,4m.
(2)设垂直于墙的长方形的边长为ym.
y×(24-4y)=32,
解得y1=2,y2=6,
当y=2时,24-4y=16;
当y=6时,24-4y=0(不合题意,舍去).
垂直于墙的长方形的边长为2m,平行于墙的一边长16m.
x(24-2x)=40,
解得x1=2,x2=10,
当x=2时,24-2x=20;
当x=10时,24-2x=4;
答:这个长方形相邻两边的长分别为2m,20m;或10m,4m.
(2)设垂直于墙的长方形的边长为ym.
y×(24-4y)=32,
解得y1=2,y2=6,
当y=2时,24-4y=16;
当y=6时,24-4y=0(不合题意,舍去).
垂直于墙的长方形的边长为2m,平行于墙的一边长16m.
点评:考查一元二次方程的应用;得到长方形的边长的代数式是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
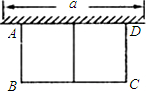 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求:
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花辅,设花圃的宽AB为x(m),面积为y(m2),求: 20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.
20、如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度a为10m)围成中间隔有一道篱笆的长方形花圃,设花圃的宽AB为xm,面积为Sm.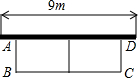 长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.
长方形养鸡场.设养鸡场的长BC为xm,面积为ym2.