题目内容
若扇形的弧长是10π，半径是15，则扇形的面积是 ．
考点：扇形面积的计算,弧长的计算
专题：
分析：先根据弧长公式求出圆心角的度数，然后求出扇形面积．
解答：解：∵L=
=10π，
∴n=120，
即圆心角为120°，
则扇形面积为：
=
=75π．
故答案为：75π．
| nπr |
| 180 |
∴n=120，
即圆心角为120°，
则扇形面积为：
| 120πr2 |
| 360 |
| 120π×152 |
| 360 |
故答案为：75π．
点评：本题考查了扇形的面积计算，解答本题的关键是根据弧长公式求出圆心角的度数，注意熟练掌握扇形面积公式和弧长公式．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列变形正确的是（ ）
| A、如果ax=by，那么x=y |
| B、如果x2=y2，那么x=y |
| C、如果ax=ay，那么x=y |
| D、如果-2x=8，那么x=-4 |
若1≤x≤3，a=
，b=
，则a、b的大小关系是（ ）
| x-1 |
| 3-x |
| A、a＞b | B、a＞b |
| C、a=b | D、以上都不对 |
一等腰三角形的两边长分别为8cm、4cm，那么该等腰三角形的周长为（ ）
| A、20cm |
| B、16cm |
| C、20cm或16cm |
| D、以上都不正确 |
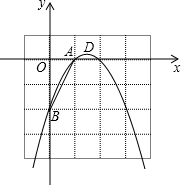如图，已知抛物线y1=-x2+bx+c经过A（1，0），B（0，-2）两点，顶点为D．