题目内容
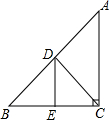 如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E是BC的中点,下面给出四个等式:(1)AB2=2BC2,(2)AB2=4DE2,(3)DC2=2DE2,(4)AC2=4DE2,其中,正确的等式有( )
如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,E是BC的中点,下面给出四个等式:(1)AB2=2BC2,(2)AB2=4DE2,(3)DC2=2DE2,(4)AC2=4DE2,其中,正确的等式有( )| A、1个 | B、2个 | C、3个 | D、4个 |
考点:等腰直角三角形
专题:
分析:由在△ABC中,∠ACB=90°,AC=BC,易证得AB2=2BC2,又由BC=2DE,即可证得AB2=4DE2,由在△DEC中,∠DEC=90°,DE=EC,易证得DC2=2DE2,由AC=2DE即可证得AC2=4DE2,即可求得答案.
解答:解:∵在△ABC中,∠ACB=90°,
∴AB2=AC2+BC2,
∵AC=BC,
∴AB2=2BC2,故①正确;
∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD⊥AB,CD=BD=AD,
∴△BDC是等腰直角三角形,
∵E是BC的中点,
∴DE⊥BC,DE=BE=CE,BC=2DE,
∵AB2=2BC2,
∴AB2=2BC=4DE2,故②正确;
∵DE⊥BC,DE=BE=CE,
∴DC2=DE2+EC2=2DE2,故③正确;
∵D是AB的中点,E是BC的中点,
∴AC=2DE,
∴AC2=4DE2,故④正确.
故选D.
∴AB2=AC2+BC2,
∵AC=BC,
∴AB2=2BC2,故①正确;
∵在△ABC中,∠ACB=90°,D是AB的中点,
∴CD⊥AB,CD=BD=AD,
∴△BDC是等腰直角三角形,
∵E是BC的中点,
∴DE⊥BC,DE=BE=CE,BC=2DE,
∵AB2=2BC2,
∴AB2=2BC=4DE2,故②正确;
∵DE⊥BC,DE=BE=CE,
∴DC2=DE2+EC2=2DE2,故③正确;
∵D是AB的中点,E是BC的中点,
∴AC=2DE,
∴AC2=4DE2,故④正确.
故选D.
点评:此题考查了直角三角形性质以及三角形中位线的性质.此题难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
用科学记数法表示-9600000正确的是( )
| A、-9.6×106 |
| B、-0.96×107 |
| C、-96×105 |
| D、9.6×106 |
下列各组图形可以通过平移互相得到的是( )
A、 |
B、 |
C、 |
D、 |
 二次函数y=ax2+bx+c的图象如图所示,则下列结论中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列结论中正确的是( )| A、a>0 |
| B、关于x的一元二次方程ax2+bx+c=3有两个相等的实数根 |
| C、c<0 |
| D、当x≥0时,y随x的增大而减小 |
8点30分时,时钟的时针与分针所夹的锐角是( )
| A、70° | B、75° |
| C、80° | D、60° |
 如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与AC、CB分别相交于点P,Q,则线段PQ长度的最小值是
如图,在△ABC中,AB=5,AC=4,BC=3,经过点C且与边AB相切的动圆与AC、CB分别相交于点P,Q,则线段PQ长度的最小值是