题目内容
18.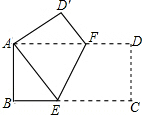 如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在D′处.若AB=3,BC=9,则折痕EF的长为( )
如图,将矩形ABCD沿EF折叠,点C落在A处,点D落在D′处.若AB=3,BC=9,则折痕EF的长为( )| A. | $\sqrt{10}$ | B. | 4 | C. | 5 | D. | 2$\sqrt{10}$ |
分析 根据翻折的性质可得AE=EC,∠AEF=∠CEF,设AE=x,表示出BE,在Rt△ABE中,利用勾股定理列方程求出x,根据两直线平行,内错角相等可得∠AFE=∠CEF,从而得到∠AEF=∠AFE,根据等角对等边可得AF=AE,过点E作EG⊥AD于G,求出AG、GF,再利用勾股定理列式计算即可得解.
解答 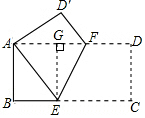 解:∵矩形ABCD沿EF折叠,点C落在A处,
解:∵矩形ABCD沿EF折叠,点C落在A处,
∴AE=EC,∠AEF=∠CEF,
设AE=x,则BE=BC-EC=9-x,
在Rt△ABE中,根据勾股定理得,AB2+BE2=AE2,
即32+(9-x)2=x2,
解得x=5,
所以,AE=5,BE=9-5=4,
∵矩形对边AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AF=AE=5,
过点E作EG⊥AD于G,则四边形ABEG是矩形,
∴AG=BE=4,
GF=AF-AG=5-4=1,
在Rt△EFG中,根据勾股定理得,EF=$\sqrt{E{G}^{2}+G{F}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.
故选A.
点评 本题考查了翻折变换的性质,矩形的性质,平行线的性质,勾股定理,翻折前后对应边相等,对应角相等,此类题目,利用勾股定理列出方程是解题的关键.

练习册系列答案
相关题目
9.2${\;}^{-\frac{1}{2}}$等于( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
13.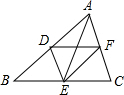 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )| A. | ∠BAC=90° | B. | BC=2AE | C. | DE平分∠AEB | D. | AE⊥BC |
3.下列计算正确的是( )
| A. | a2•a=2a3 | B. | a2•a3=2a6 | C. | (-2a3)2=4a6 | D. | a8÷a2=a4 |
10.下列说法中正确的是( )
| A. | 了解一批日光灯的使用寿命适宜采用抽样调查 | |
| B. | “打开电视,正在播放《沈视早报》”是必然事件 | |
| C. | 数据1,1,2,2,3的众数是3 | |
| D. | 一组数据的波动越大,方差越小 |
7.函数y=$\frac{1}{\sqrt{x-1}}$中,自变量x的取值范围是( )
| A. | x≥1 | B. | x>1 | C. | x<1 | D. | x≤1 |
8.据统计,2016年某市的初中毕业生人数约有43900人,这个数字用科学记数法可以表示为( )
| A. | 4.39×105 | B. | 43.9×103 | C. | 4.39×104 | D. | 0.439×105 |
 如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.
如图,已知抛物线y=-x2+9的顶点为A,曲线DE是双曲线y=$\frac{k}{x}$(3≤x≤12)的一部分,记作G1,且D(3,m)、E(12,m-3),将抛物线y=-x2+9水平向右移动a个单位,得到抛物线G2.