题目内容
【题目】已知在△ABC中，∠A＝∠B＝30°．
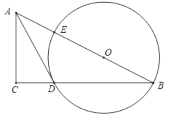
（1）尺规作图：在线段AB上找一点O，以O为圆心作圆，使⊙O经过A，C两点；
（2）在（1）中所作的图中，求证：BC是⊙O的切线．
【答案】（1）见解析；（2）见解析
【解析】
(1)作AC的垂直平分线MN交AB于点O，以O为圆心，OA为半径作⊙O即可．
(2)根据题目中给的已知条件结合题(1)所作的图综合应用证明∠OCB＝90°即可解决问题．
(1)解：如图，⊙O即为所求．
(2)证明：连接OC．
∵∠A＝∠B＝30°，
∴∠ACB＝180°﹣30°﹣30°＝120°，
∵MN垂直平分相对AC，
∴OA＝OC，
∴∠A＝∠ACO＝30°，
∴∠OCB＝90°，
∴OC⊥BC，
∴BC是⊙O的切线．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
