题目内容
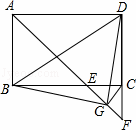
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若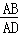 =
= ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.
其中正确的结论是 .(填写所有正确结论的序号)
①③④. 解:∵AE平分∠BAD,
∴∠BAE=45°,
∴△ABE是等腰直角三角形,
∴AB=BE,∠AEB=45°,
∵AB=CD,
∴BE=CD,
故①正确;
∵∠CEF=∠AEB=45°,∠ECF=90°,
∴△CEF是等腰直角三角形,
∵点G为EF的中点,
∴CG=EG,∠FCG=45°,
∴∠BEG=∠DCG=135°,
在△DCG和△BEG中,
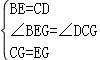 ,
,
∴△DCG≌△BEG(SAS).
∴∠BGE=∠DGC,
∵∠BGE<∠AEB,
∴∠DGC=∠BGE<45°,
∵∠CGF=90°,
∴∠DGF<135°,
故②错误;
∵∠BGE=∠DGC,
∴∠ABG+∠ADG=∠ABC+∠CBG+∠ADC﹣∠CDG=∠ABC+∠ADC=180°,
故③正确;
∵△DCG≌△BEG,
∵∠BGE=∠DGC,BG=DG,
∵∠EGC=90°,
∴∠BGD=90°,
∵BD=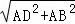 =
=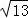 ,
,
∴BG=DG=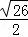 ,
,
∴S△BDG=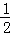 ×
×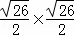 =
=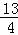
∴3S△BDG=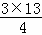 ,
,
过G作GM⊥CF于M,
∵CE=CF=BC﹣BE=BC﹣AB=1,
∴GM=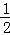 CF=
CF=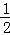 ,
,
∴S△DGF=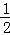 •DF•GM=
•DF•GM=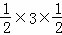 =
=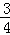 ,
,
∴13S△DGF=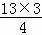 ,
,
∴3S△BDG=13S△DGF,
故④正确.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 数法表示为( )
数法表示为( ) A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).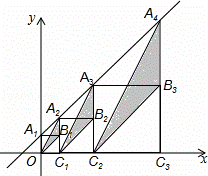
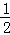
 x﹣1=0有两个不相等的实数根,则k的取值范围是 .
x﹣1=0有两个不相等的实数根,则k的取值范围是 .
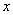 的分式方程
的分式方程 无解,则
无解,则 =__________.
=__________.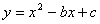 交
交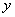 轴于点B,对称轴是
轴于点B,对称轴是