题目内容
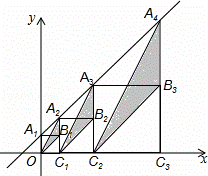
在直角坐标系中,直线y=x+1与y轴交于点 A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左导游依次记为S1、S2、S3、…Sn,则Sn的值为 (用含n的代数式表示,n为正整数).
22n﹣3
| 考点: | 一次函数图象上点的坐标特征;正方形的性质.. |
| 专题: | 规律型. |
| 分析: | 根据直线解析式先求出OA1=1,得出第一个正方形的边长为1,求得A2B1=A1B1=1,再求出第一个正方形的边长为2,求得A3B2=A2B2=2,第三个正方形的边长为22,求得A4B3=A3B3=22,得出规律,根据三角形的面积公式即可求出Sn的值. |
| 解答: | 解:∵直线y=x+1,当x=0时,y=1,当y=0时,x=﹣1, ∴OA1=1,OD=1, ∴∠ODA1=45°, ∴∠A2A1B1=45°, ∴A2B1=A1B1=1, ∴S1= ∵A2B1=A1B1=1, ∴A2C1=2=21, ∴S2= 同理得:A3C2=4=22,…, S3= ∴Sn= 故答案为:22n﹣3. |
| 点评: | 本题考查了一次函数图象上点的坐标特征以及正方形的性质;通过求出第一个正方形、第二个正方形和第三个正方形的边长得出规律是解决问题的关键. |

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
2015年某中学举行的春季田径径运动会上,参加男子跳高的15名运动员的成绩如表所示:
| 成绩(m) | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
| 人数 | 1 | 2 | 4 | 3 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
|
| A. | 1.70m,1.65m | B. | 1.70m,1.70m | C. | 1.65m,1.60m | D. | 3,4 |
 ×1×1=
×1×1= ×(22)2=23
×(22)2=23

 上任取异于B、C的一点D,连接DA,DB;
上任取异于B、C的一点D,连接DA,DB;
 ﹣1|+20120﹣(﹣
﹣1|+20120﹣(﹣ )﹣1﹣3tan30°.
)﹣1﹣3tan30°. 中,最小的是
中,最小的是  取1.732,结果保留整数)
取1.732,结果保留整数)
 )﹣2=4 D. (﹣2)0=﹣1
)﹣2=4 D. (﹣2)0=﹣1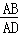 =
= ,则3S△BDG=13S△DGF.
,则3S△BDG=13S△DGF.