Question

【题目】如图，在每个小正方形的边长为的网格中，点，，，均在格点上，与相交于点．

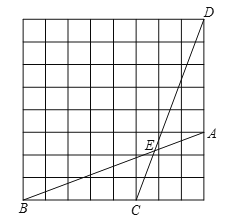
（1）的长等于 ；

（2）是线段上一点，且，在线段上有一点，满足，请在如图所示的网格中，用无刻度的直尺，画出点，并简要说明点的位置是如何找到的（不要求证明） ．

Answer 1

【答案】（1）；（2）图见解析；取格点G、H，连接GH与CD 相交于点 F，连接 BF，BD，取格点 I、J，连接 IJ 与 BD交于点 K，连接EK与 BF交于点P，点 P即为所求．

【解析】

（1）根据勾股定理计算即可；

（2）求出，然后作出DF＝EC，可得，即可得到点F，然后取格点 I、J，连接 IJ 与 BD交于点 K，连接EK与 BF交于点P，作FM∥EK，根据平行线分线段成比例定理求出，进而得到，再利用平行线分线段成比例定理即可得到，故点 P为所求．

解：（1）由勾股定理得：CD；

（2）如图，取格点G、H，连接GH与CD 相交于点 F，连接 BF，BD，取格点 I、J，连接 IJ 与 BD交于点 K，连接EK与 BF交于点P，点 P即为所求．

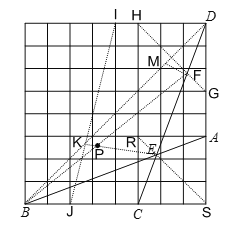
证明：如图，由图易得EA＝EC，

∴点E在直线RS上，

∵RC∥DS，且，

∴，

取格点G、H，连接GH与CD 相交于点 F，则DF＝EC，

∴，

∴，即，

取格点 I、J，连接 IJ 与 BD交于点 K，连接EK与 BF交于点P，

∵BS∥ID，，

∴，

作FM∥EK，则，

∴设BK＝4a，则DK＝8a，DM＝3a，MK＝5a，

∴，

∵FM∥EK，

∴．