Question

【题目】在平面直角坐标系中，为坐标原点，抛物线的顶点为，与轴的交点为．

（1）求点，的坐标；

（2）已知点(4，2)，将抛物线向上平移得抛物线，点平移后的对应点为，且，求抛物线的解析式；

（3）将抛物线：沿轴翻折，得抛物线，抛物线与轴交于点，（点在点的左侧），与轴交于点，平行于轴的直线与抛物线交于点(，)，(，)，与直线交于点(，)，若＜＜，结合函数的图象，求的取值范围．

Answer 1

【答案】（1）M（－2，－1），N（0，3）；（2）抛物线的解析式为：；（3）．

【解析】

（1）将解析式化成顶点式可得M的坐标，求出x＝0时y的值可得N的坐标；

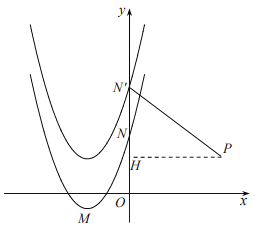
（2）设抛物线的解析式为：，则，过点P作PH⊥于点H，可得PH＝4，N′H＝m－2，根据勾股定理构建方程求出m即可；

（3）求出抛物线的解析式，可得点A、B、D的坐标及的值，求出直线BD的解析式，根据结合函数图象可得的取值范围，进而可得答案．

解：（1）∵，

∴M（－2，－1），

当x＝0时，，

∴N（0，3）；

（2）设抛物线的解析式为：，则，

过点P作PH⊥于点H，

∵(4，2)，

∴PH＝4，N′H＝m－2，

∵，

∴，

解得：，

∴抛物线的解析式为：；

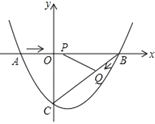
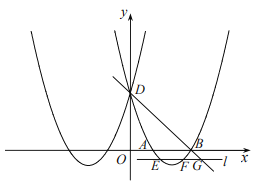
（3）∵抛物线的顶点坐标为（－2，－1），

∴抛物线的顶点坐标为（2，－1），

∴抛物线的解析式为：，

令y＝0，得，

解得：，，

∴A（1，0），B（3，0），

令x＝0，得，

∴D（0，3），

设直线BD的解析式为：y＝kx＋b（k≠0），

则，解得：，

∴直线BD的解析式为：y＝－x＋3，

∵抛物线的对称轴为：，

∴，

令y＝－x＋3＝－1，解得：x＝4，

∵，

结合函数图象得：，

∴，

即的取值范围为：．