Question

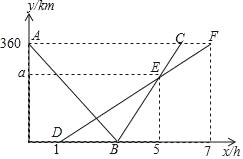
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发，匀速行驶，先相向而行，慢车在快车出发1h后出发，到达佳市后停止行驶，快车到达哈市后，立即按原路原速返回佳市（快车调头的时间忽略不计），快、慢两车距哈市的路程y1（单位：km），y2（单位：km）与快车出发时间x（单位：h）之间的函数图象如图所示，请结合图象信息解答下列问题：

（1）直接写出慢车的行驶速度和a的值；

（2）快车与慢车第一次相遇时，距离佳市的路程是多少千米？

（3）快车出发多少小时后两车相距为100km？请直接写出答案．

Answer 1

【答案】（1）慢车的速度为60km/h，a的值为240；（2）快车与慢车第一次相遇时，距离佳市的路程是280千米；（3）快车出发、或小时后两车相距为100km．

【解析】

1）根据速度＝路程÷时间可求出慢车的速度，再根据路程＝速度×时间可求出a值.

2）根据路程一速度时间时间分段），可得出AB、BC、DF段的函数解析式，当AB、DF段的函数解析式y值相等时，可求出快车与慢车第一次相遇时距离佳市的路程.

3）由当x＝1时AB段的y值大于100和当z＝6时DF段的y值小于100，可确定分1≤ェ≤3和3≤x≤6两种情况考虑，根据两车相距100km可列出关于x的含绝对值符号的一元一次方程，解之即可得出结论.

（1）慢车的速度为360÷（7﹣1）=60（km/h），

a=60×（5﹣1）=240．

答：慢车的速度为60km/h，a的值为240．

（2）快车的速度为（360+240）÷5=120（km/h）．

根据题意得：AB段的解析式为y=360﹣120x（0≤x≤3）；

BC段的解析式为y=120（x﹣3）=120x﹣360（3≤x≤6）；

DF段的解析式为y=60（x﹣1）=60x﹣60（1≤x≤7）．

当y=360﹣120x=60x﹣60时，x=，

此时y=60x﹣60=60×﹣60=80，

∴360﹣80=280（km）．

答：快车与慢车第一次相遇时，距离佳市的路程是280千米．

（3）当x=1时，y=360﹣120x=240＞100，

当x=6时，y=60x﹣60=300，360﹣300=60＜100，

∴分1≤x≤3和3≤x≤6两种情况考虑．

当1≤x≤3时，有|360﹣120x﹣（60x﹣60）|=100，

解得：x1=，x2=；

当3≤x≤6时，有|60x﹣60﹣（120x﹣360）|=100，

解得：x3=，x4=（舍去）．

综上所述：快车出发、或小时后两车相距为100km．