题目内容
如图16,在平面直角坐标系中,以坐标原点O为圆心,2为半径画⊙O,P是⊙O上一动点,且P在第一象限内,过点P作⊙O的切线与x轴相交于点A,与y轴相交于点B.
(1)点P在运动时,线段AB的长度也在发生变化,请写出线段AB长度的最小值,并说明理由;
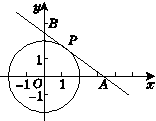
(2)在⊙O上是否存在一点Q,使得以Q,O,A,P为顶点的四边形是平行四边形?若存在,请求出Q点的坐标;若不存在,请说明理由.
解:(1)线段AB长度的最小值为4.
理由如下:
连接OP,如答图8所示.

答图8
∵AB切⊙O于P,
∴OP⊥AB.
取AB的中点C,
则AB=2OC;
当OC=OP时,OC最短,
即AB最短,
此时AB=4.
(2)设存在符合条件的点Q.

答图9
如答图9,设四边形APOQ为平行四边形,
∵∠APO=90°,
∴四边形APOQ为矩形,
又∵OP=OQ,
∴四边形APOQ为正方形,
∴OQ=QA,∠QOA=45°.
在Rt△OQA中,
根据OQ=2,∠AOQ=45°,
得Q点坐标为( ,-
,- );
);
如答图10,设四边形APQO为平行四边形,

答图10
∵OQ∥PA,∠APO=90°,
∴∠POQ=90°,
又∵OP=OQ,
∴∠PQO=45°,
∵PQ∥OA,
∴PQ⊥y轴.
设PQ⊥y轴于点H,
在Rt△OHQ中,根据OQ=2,∠HQO=45°,
得Q点坐标为(- ,
, ).
).
∴符合条件的点Q的坐标为(- ,
, )或(
)或( ,-
,- ).
).

练习册系列答案
相关题目
 D.60,
D.60,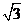


 B.
B.  C.
C. 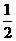 D.
D. 

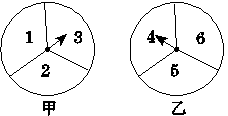
 D.4
D.4