题目内容
13.若实数a、b、c满足abc≠0,且a+b-c=0,求$\frac{{{b^2}+{c^2}-{a^2}}}{2bc}+\frac{{{c^2}+{a^2}-{b^2}}}{2ac}+\frac{{{a^2}+{b^2}-{c^2}}}{2ab}$的值.分析 把c=a+b代入原式的分子,利用完全平方公式展开,合并同类项,约分即可解决问题.
解答 解:∵a+b-c=0,
∴c=a+b,
∴原式=$\frac{{b}^{2}+{a}^{2}+2ab+{b}^{2}-{a}^{2}}{2bc}$+$\frac{{a}^{2}+2ab+{b}^{2}+{a}^{2}-{b}^{2}}{2ac}+$$\frac{{a}^{2}+{b}^{2}-({a}^{2}+2ab+{b}^{2})}{2ab}$
=$\frac{2{b}^{2}+2ab}{2bc}$+$\frac{2{a}^{2}+2ab}{2ac}$-1
=$\frac{b+a}{c}+\frac{a+b}{c}$-1
=1+1-1
=1.
点评 本题考查分式的化简求值,解题的关键是利用完全平方公式展开,体现了整体代入的解题思想,学会灵活应用a+b=c这个条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数$y=\frac{x}{x+3}$中,自变量x的取值范围是( )
| A. | x>-3 | B. | x<-3 | C. | x≠-3 | D. | x≠3 |
5.若x2+mx+25是完全平方式,则m的值等于( )
| A. | 10 | B. | -10 | C. | 10或-10 | D. | 20 |
2.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 明天下雪的概率为$\frac{1}{2}$,表示明天有半天都在下雪 | |
| C. | 甲、乙两人在相同条件下各射击10次,他们成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 了解一批充电宝的使用寿命,适合用普查的方式 |
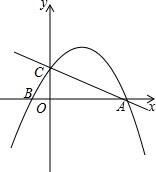 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+2$的图象与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c关于直线x=$\frac{3}{2}$对称,且经过A、C两点,与x轴交于另一点为B.