题目内容
11.先化简,再求值:已知m=2+$\sqrt{3}$,求$\frac{{{m^2}-1}}{m+1}-\frac{{\sqrt{{m^2}-2m+1}}}{{m-{m^2}}}$的值.分析 首先将原式的分子与分母分解因式,进而化简求出答案.
解答 解:原式=$\frac{(m+1)(m-1)}{m+1}$-$\frac{\sqrt{(m-1)^{2}}}{m(1-m)}$
=m-1+$\frac{1}{m}$
则原式=2+$\sqrt{3}$-1+$\frac{1}{2+\sqrt{3}}$
=3.
点评 此题主要考查了二次根式的化简求值,正确化简分式是解题关键.

练习册系列答案
相关题目
1.我县某初中学校举办“经典诵读”比赛,13名学生进入决赛,他们所得分数互不相同,比赛共设7个获奖名额,某学生知道自己的分数后,要判断自己能否获奖,他应该关注的统计量是( )
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 方差 |
2.下列各曲线中,不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
16.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{3}$ |

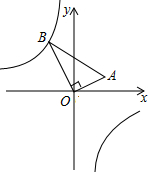 如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.
如图,在△AOB中,∠AOB=90°,点A的坐标为(2,1),BO=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值为-8.