题目内容
如图,△ABC是等边三角形,点D是边BC上(除B、C外)的任意 一点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E.
一点,∠ADE=60°,且DE交△ABC外角∠ACF的平分线CE于点E.
(1)求证:∠1=∠2;
(2)求证:AD=DE.
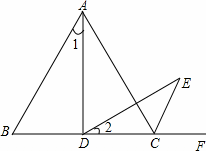
详解:(1)∵△ABC是等边三角形,∠ADE=60°
∴∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
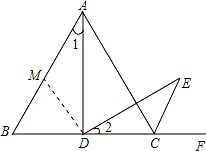
(2)如图,在AB上取一点M,使BM=BD,连接MD.
∵△ABC是等边三角形
∴∠B=60°
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是△AB C外角∠ACF的平分线,
C外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE,
∵BABM=BCBD,即MA=CD.
在△AMD和△DCE中
∠1=∠2,AM=DC,∠AMD=∠DCE,
∴△AMD≌△DCE(ASA).
∴AD=DE.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
九年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学答题比赛,共10题,答对题数统计如表一:
(表一)
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
(表二)
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
(1)根据表一中统计的数据,完成表二;
(2)请你从平均数和方差的角度分析,哪组的成绩更好些?
 CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )
CB的平分线交于点E,过点E作MN∥BC交AB于M,交AC于N,若BM+CN=9,则线段MN的长为( )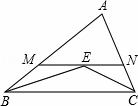

 经过两次下调后,决定以每平方米4860元的均价开盘销售.
经过两次下调后,决定以每平方米4860元的均价开盘销售.