题目内容
已知：如图，在平行四边形ABCD中，点E、F分别在AB、DC上，AE=CF．
求证：∠ADE=∠CBF．
证明：∵四边形ABCD为平行四边形，
∴AD=CB，
∠A=∠C．
在△AED和△CFB中，
∴△AED≌△CFB．
∴∠ADE=∠CBF．
分析：根据平行四边形的性质，可证△AED≌△CFB，继而得出结论．
点评：本题考查了平行四边形的性质及全等三角形的判定与性质，属于基础题，注意掌握全等三角形的判定定理．
∴AD=CB，
∠A=∠C．
在△AED和△CFB中，
∴△AED≌△CFB．
∴∠ADE=∠CBF．
分析：根据平行四边形的性质，可证△AED≌△CFB，继而得出结论．
点评：本题考查了平行四边形的性质及全等三角形的判定与性质，属于基础题，注意掌握全等三角形的判定定理．
练习册系列答案
相关题目
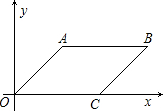如图，在平行四边形ABC0中，已知点A、C两点的坐标为A（
（2013•南平模拟）如图，已知四边形ABCD．请在下列四个关系中，选出两个恰当的关系作为条件，推出四边形ABCD是平行四边形，并予证明．
如图，在平行四边形OABC中，已知点A、C两点的坐标为A （
3，
，将∠OBA对折，使点O的对应点H恰好落在直线AB上，折痕交x轴于点C，