题目内容
20.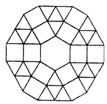 某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.)
某广场地面图案的一部分如图所示,图案的中央是一块正六边形的地砖,周围用正三角形和正六边形的地砖密铺,环绕正六边形的那些正三角形和正方形为第一层,环绕第一层的那些正三角形和正方形为第二层,这样从里到外共铺了10层,每一层的外边界构成一个多边形,(注:多边形是由一些线段首尾顺次连接的封闭平面图形,各条线段是多边形的边;正六边形的各边长相等.) 已知中央正六边形地砖的边长为0.6米,试写出外边界所成多边形的周长y与层数n之间的函数解析式;并求第十层外边界所成多边形的周长.
分析 由图形可知:从里向外的第1层是6×1+6=12边形,第2层是6×2+6=18边形,…每层都比前一层多6条边,依此递推,从而得出外边界所成多边形的周长y与层数n之间的函数解析式,再把10代入求出边数,再根据正六边形地砖的边长,即可得出答案.
解答 解:根据题意得:从里向外的第1层是6×1+6=12边形,
第2层是6×2+6=18边形.
此后,每层都比前一层多6条边.
依此递推,第10层是6×10+6=66边形,
则外边界所成多边形的周长y与层数n之间的函数解析式是:y=6n+6,
∵边长为0.6m,
∴第10层的外边界所围成的多边形的周长是66×0.6=39.6米.
点评 此题考查图形的变化规律,分别找到三角形和正方形的个数的规律是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
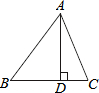 如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.
如图所示,在△ABC中,AD是BC边上的高,AB=15,AC=13,AD=12,根据上述数据,你能求得△ABC的面积吗?试试看.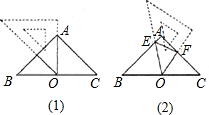 在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.
在△ABC中,AB=AC=2,∠BAC=90°,取一块含45°角的直角三角形纸板,将45°角的顶点放在斜边BC的中点O处(如图①),顺时针方向旋转三角尺,使45°角的两边与AB、AC分别交于点E、F(如图②).设BE=x,CF=y,求y与x的函数表达式,并写出x的取值范围.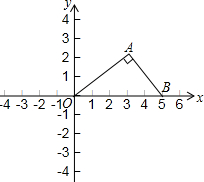 如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.
如图所示,在平面直角坐标系内有A、B两点,△A0B中∠OAB=90°,AO=4,AB=3,BO=5,点A横坐标与点B横坐标的比为16:25.
 ,其中
,其中 是
是 之间的整数,请选一个合适的
之间的整数,请选一个合适的 求解.
求解. 时,去分母后变形为( )
时,去分母后变形为( ) B.
B. 
 D.
D. 
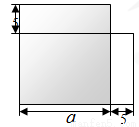
 米的正方形土地租给赵老汉栽种.过了一年,他对赵老汉说:“我把你这块地的一边减少5米,另一边增加5米,继续租给你,租金不变,你也没吃亏,你看如何?”赵老汉一听,觉得好像没吃亏,就答应了. 同学们,你们觉得赵老汉有没有吃亏?请说明理由.
米的正方形土地租给赵老汉栽种.过了一年,他对赵老汉说:“我把你这块地的一边减少5米,另一边增加5米,继续租给你,租金不变,你也没吃亏,你看如何?”赵老汉一听,觉得好像没吃亏,就答应了. 同学们,你们觉得赵老汉有没有吃亏?请说明理由.