Question

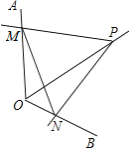
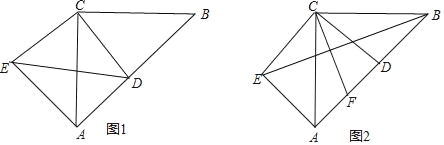
【题目】如图1，在△ABC中，∠ACB=90°，AC=BC，D为AB上一点，连接CD，将CD绕点C顺时针旋转90°至CE，连接AE．

（1）连接ED，若CD=，AE=4，求AB的长；

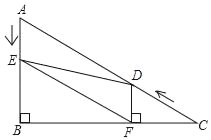
（2）如图2，若点F为AD的中点，连接EB、CF，求证：CF⊥EB．

Answer 1

【答案】（1）；（2）见解析

【解析】分析：（1）根据旋转的性质，得出△BCD≌△ACE，进而得到AE=BD=4，∠CAE=∠B=45°=∠CAB，∠EAD=90°，再根据CD2+EC2=DE2=AE2+AD2，即可得到AD的长，进而得出AB的长；

（2）过C作CG⊥AB于G，则AG=BG，根据等腰直角三角形的性质，即可得到，再根据点F为AD的中点，即可得到，再根据，∠CGF=∠BAE=90°，即可判定△CGF∽△BAE，进而得到∠FCG=∠ABE，依据∠ABE+∠∠CFG=90°，可得CF⊥BE．

详解：（1）如图1，由旋转可得：EC=DC=，∠ECD=90°=∠ACB，∴∠BCD=∠ACE．

又∵AC=BC，∴△BCD≌△ACE，∴AE=BD=4，∠CAE=∠B=45°=∠CAB，∴∠EAD=90°．

∵CD2+EC2=DE2=AE2+AD2，∴AD==，∴AB=AD+DB=+4；

（2）如图2，过C作CG⊥AB于G，则AG=AB．

∵∠ACB=90°，AC=BC，∴CG=AB，即．

∵点F为AD的中点，∴FA=AD，∴FG=AG﹣AF=AB﹣AD=（AB﹣AD）=BD，由（1）可得：BD=AE，∴FG=AE，即．

又∵∠CGF=∠BAE=90°，∴△CGF∽△BAE，∴∠FCG=∠ABE．

∵∠FCG+∠CFG=90°，∴∠ABE+∠∠CFG=90°，∴CF⊥BE．