题目内容
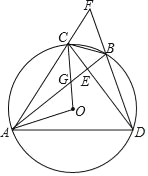
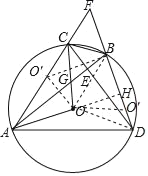
【题目】如图,△ABC内接于⊙O,过点C作CD⊥AB于点E,交⊙O于点D,延长AC交DB延长线于点F,BF=![]() ,连接AO、CO.CO与AB相交于点G,∠CGE=3∠CAB,OC=10,将圆心O绕着点B旋转得到点O′,若点O′恰好落△ADF某一边上时,则OO′的长度为_____.
,连接AO、CO.CO与AB相交于点G,∠CGE=3∠CAB,OC=10,将圆心O绕着点B旋转得到点O′,若点O′恰好落△ADF某一边上时,则OO′的长度为_____.
【答案】![]()
【解析】
延长AO交BD于H,连接OB,OD,根据全等三角形的性质得到AB=AD,推出AH垂直平分BD,根据平行线分线段成比例得到![]() ,根据勾股定理得到OO′=
,根据勾股定理得到OO′=![]() =4
=4![]() ,过O作OO′⊥AB于K交AF于O′,根据菱形的性质得到O′B=OB=5,再根据勾股定理即可得到结论.
,过O作OO′⊥AB于K交AF于O′,根据菱形的性质得到O′B=OB=5,再根据勾股定理即可得到结论.
解:延长AO交BD于H,连接OB,OD,
∵∠ADC=![]() ∠AOC=
∠AOC=![]() (180°﹣∠OAC﹣∠OCA)=
(180°﹣∠OAC﹣∠OCA)=![]() (180°﹣4∠CAB)=90°﹣2∠CAB,
(180°﹣4∠CAB)=90°﹣2∠CAB,
∴∠DAB=90°﹣∠ADC=2∠CAB=2∠OAB,
∴∠OAD=∠OAB,∵OA=OB=OD,
∴∠OBA=∠OAB=∠OAD=∠ODA,
∴∠AOB=∠AOD,
在△OAB与△OAD中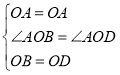 ,
,
∴△OAB≌△OAD,
∴AB=AD,
∵∠OAB=∠OAD,
∴AH垂直平分BD,
∵∠OBA=∠OAB=∠BAC,
∴OB∥AF,
∴![]() ,
,
令OH=4a,则BH=3a,OB=5a=10,∴a=2,
∴BD=2BH=12,
当O′在BD上时,O′H=O′B﹣BH=4,
∴OO′=![]() =4
=4![]() ,
,
过O作OO′⊥AB于K交AF于O′,
则四边形OAO′B是菱形,
∴O′B=OB=5,BK=![]() AB=3
AB=3![]() ,
,
∴OK=![]() =
=![]() ,
,
∴OO′=2OK=2![]() .
.
故答案为:4![]() 或2
或2![]() .
.

 出彩同步大试卷系列答案
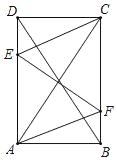
出彩同步大试卷系列答案【题目】已知:如图,矩形ABCD的对角线AC与BD相交于点O,点O关于直线AD的对称点是E,连接AE、DE.
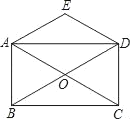
(1)试判断四边形AODE的形状,不必说明理由;
(2)请你连接EB、EC,并证明EB=EC.
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.