Question

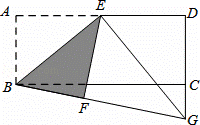
如图，在矩形ABCD中，E是AD的中点，把矩形沿BE折叠，使点A落在矩形外的一点F上，连接BF并延长交DC的延长线于点G．

（1）求证：△EFG≌△EDG．

（2）当DG=3，BC=2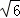时，求CG的长．

Answer 1

              （1）证明：E是边AD的中点，

∴DE=AE=FE，

又∵四边形ABCD是矩形，

∴∠D=∠A=∠BFE=90°

∴∠D=∠EFG=90°．

在Rt△EFG与Rt△EDG中，

，

∴Rt△EFG≌Rt△EDG（HL）；

（2）解：∵△EFG≌△EDG，

∴DG=FG=3，

设CG=x，DC=3﹣x，

AB=BF=DC=3﹣x

BG=3﹣x+3=6﹣x

在Rt△BCG中，

BG²=BC²+CG²，

（6﹣x）²=（2）²+x²，

解得x=1，

即CG=1．