题目内容
已知命题:“P是等边三角形ABC内的一点,若P到三边的距离相等,则PA=PB=PC.”证明这个命题,并写出它的逆命题.判断其逆命题成立吗?若成立,请给出证明.
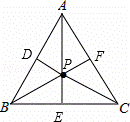
解:如图,已知P是等边三角形ABC内的一点,PD⊥AB于D,PE⊥BC于E,PF⊥AC于F,PD=PE=PF.求证:PA=PB=PC.
证明:∵PD⊥AB于D,PE⊥BC于E,PD=PE,
∴BP平分∠ABC,
∵BA=BC,
∴BP是AC的垂直平分线,
同理,AP是BC的垂直平分线,CP是AB的垂直平分线,
∴P是△ABC三边垂直平分线的交点,
∴PA=PB=PC.
逆命题:P是等边三角形ABC内的一点,若PA=PB=PC,则P到三边的距离相等.其逆命题成立.
证明:∵PA=PB,
∴P在AB的垂直平分线上,
∵AC=BC,
∴C在AB的垂直平分线上,
∴CP是AB的垂直平分线,
∴CP平分∠ACB,
同理,BP平分∠ABC,AP平分∠BAC,
∴P是△ABC三个角的角平分线的交点,
∴PD=PE=PF.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
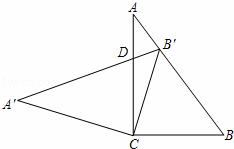
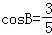 ,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么
,把这个直角三角形绕顶点C旋转后得到Rt△A′B′C,其中点B′正好落在AB上,A′B′与AC相交于点D,那么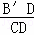 = .
= .
 请用直尺和圆规作出∠AOB的平分线(要求保留作图痕迹,不写作法).
请用直尺和圆规作出∠AOB的平分线(要求保留作图痕迹,不写作法). 
 矩形的对角线相等且互相垂直平分
矩形的对角线相等且互相垂直平分
 时,求CG的长.
时,求CG的长.