题目内容
6.已知二次函数y=x2-x-6.(1)画出函数的图象;
(2)观察图象,指出方程x2-x-6=0的解及不等式x2-x-6>0解集.
分析 (1)求出抛物线与坐标轴的交点坐标,然后画出大致图象即可;
(2)根据函数图象,抛物线与x轴的交点坐标写出方程的解;函数图象上方部分的x的取值范围即为不等式的解集.
解答 解:(1)令y=0,则x2-x-6=0,
解得x1=-2,x2=3,
所以,抛物线与x轴的交点坐标为(3,0),(-2,0),
令x=0,则y=-6,
所以,抛物线与y轴的交点坐标为(0,-6),
函数图象如图;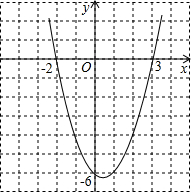
(2)由抛物线解析式y=x2-x-6知,抛物线与x轴的交点坐标是(3,0),(-2,0),
所以,方程x2-x-6=0的解是x1=-2,x2=3;
不等式x2-x-6>0的解集为x<-2或x>3.
点评 本题考查了二次函数与不等式组,抛物线与x轴的交点问题,数形结合是数学中的重要思想之一,解决函数问题更是如此,同学们要引起重视.

练习册系列答案
相关题目
14.使代数式$\frac{2x-1}{x-1}$的值为0的x值是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
