题目内容
10. 如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
分析 (1)首先证明FG∥DB,GH∥EC,由平行线的性质可知∠DBE=∠FGE,∠EHG=∠AEG,从而可证明∠FGH=90°;
(2)连接FM、HM.首先证明四边形FGHM为矩形,然后利用勾股定理求解即可.
解答 解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EHG=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°-∠A=180°-90°=90°.
(2)如图所示:连接FM、HM.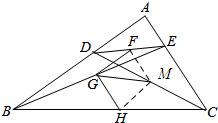
∵M、H分别是BC和DC的中点,
∴MN∥BD,MN=$\frac{1}{2}BD$.
同理:GF∥BD,GF=$\frac{1}{2}BD$.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH=$\frac{1}{2}EC$=3,$HM=\frac{1}{2}BD=4$,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM=$\sqrt{G{H}^{2}+H{M}^{2}}=\sqrt{{3}^{2}+{4}^{2}}$=5.
点评 本题主要考查的是三角形的中位线定理、平行四边形的判定、矩形的判定、勾股定理、平行线的性质的综合应用,证得四边形FGHM是矩形是解题的关键.

练习册系列答案
相关题目
18.式子$\frac{2x+1}{\sqrt{x-1}}$有意义的x的取值范围是( )
| A. | x<1 | B. | x≠1 | C. | x≥1 | D. | x>1 |
15.如图,小明的父母出去散步,从家走了20分钟到一个离家900米的报亭,母亲随即按原速度返回家,父亲在报亭看了10分钟报纸后,用15分钟返回家,则分别表示父亲、母亲离家距离与时间之间关系的是( )
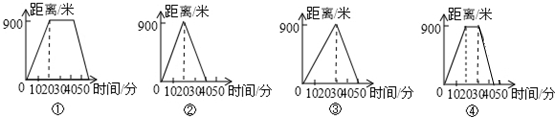

| A. | ①③ | B. | ①② | C. | ④② | D. | ④③ |
2.某校初一年级到礼堂开会,若每条长凳坐5人,则少10条长凳;若每条长凳坐6人,则又多余2条长凳.如果设学生数为x人,长凳为y条,根据题意可列方程组( )
| A. | $\left\{\begin{array}{l}{x=5y+5×10}\\{x=6y-6×2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=5y-5×10}\\{x=6y+6×2}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{x=5y-10}\\{x=6y+2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=5y+10}\\{x=6y-2}\end{array}\right.$ |
19.某市2013年投入教育经费2亿元,为了发展教育事业,该市每年教育经费的年增长率均为x,从2013年到2015年共投入教育经费9.5亿元,则下列方程正确的是( )
| A. | 2x2=9.5 | B. | 2(1+x)=9.5 | ||
| C. | 2(1+x)2=9.5 | D. | 2+2(1+x)+2(1+x)2=9.5 |
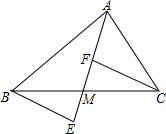 如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.
如图,M是△ABC的边BC上一点,△BME旋转后能与△CMF重合,已知∠ABC=∠ACF,∠EBM=28°,∠ACB=66°,求∠BAC的度数.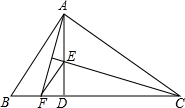 如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.
如图,已知在Rt△ABC中,∠BAC=90°,AD⊥BC于D,CE为∠ACB的平分线交AD于E,AF为∠BAD的平分线,交BC于F,求证:△ACE≌△FCE.