题目内容
11．
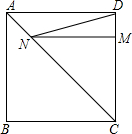正方形ABCD的边长为3，M是DC上一点，且DM=1，N是对角线AC上的一动点，求DN+MN的最小值．
分析 要求DN+MN的最小值，DN，MN不能直接求，可考虑通过作辅助线转化DN，MN的值，从而找出其最小值求解．
解答 解：如图，连接BM，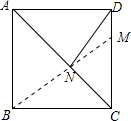
∵点B和点D关于直线AC对称，
∴NB=ND，
则BM就是DN+MN的最小值，
∵正方形ABCD的边长是3，DM=1，
∴CM=2，
∴BM=$\sqrt{B{C}^{2}+C{M}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$，
∴DN+MN的最小值是$\sqrt{13}$．
点评 本题考查了正方形的性质、轴对称的性质以及勾股定理等知识的综合应用，解题的难点在于确定满足条件的点N的位置：利用轴对称的方法．然后熟练运用勾股定理．
练习册系列答案
名校联盟快乐课堂系列答案
黄冈创优卷系列答案
相关题目
1．顺次连接菱形ABCD各边中点所得到的四边形一定是（ ）
| A． | 菱形 | B． | 正方形 | ||
| C． | 矩形 | D． | 对角线互相垂直的四边形 |
如图，AB交CD于O，OE⊥AB．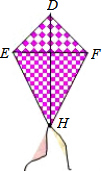
为参加学校举办的风筝设计比赛，小明用四根竹棒扎成如图所示的风筝框架，其中∠EDH=∠FDH，ED=FD．将上述条件标注在图中，小明不用测量就能知道EH=FH吗？为什么？
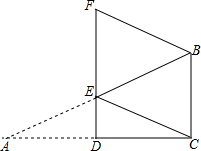如图，在直角三角形纸片ABC中，∠ACB=90°，把这张纸片沿DE折叠，使点A与C重合，连接CE，过点B作CE的平行线，与DE的延长线交于点F．