题目内容
13. 如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )
如图,在△ABC中,AD平分∠BAC,DE⊥AB于E,S△ABC=15,DE=3,AB=6,则AC长是( )| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
分析 先求出△ABD的面积,再得出△ADC的面积,最后根据角平分线上的点到角的两边的距离相等可得AC边上的高,从而得解.
解答 解:∵DE=3,AB=6,
∴△ABD的面积为$\frac{1}{2}×3×6=9$,
∵S△ABC=15,
∴△ADC的面积=15-9=6,
∵AD平分∠BAC,DE⊥AB于E,
∴AC边上的高=DE=3,
∴AC=6×2÷3=4,
故选D.
点评 本题考查了角平分线上的点到角的两边的距离相等的性质,熟记性质是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
1.直线y=$\frac{1}{2}$x+b与直线y=-2x+2的交点不可能在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.把抛物线y=-$\frac{1}{2}$x2向下平移1个单位,再向左平移1个单位,得到的抛物线解析式为( )
| A. | y=-$\frac{1}{2}$(x+1)2+1 | B. | y=-$\frac{1}{2}$(x+1)2-1 | C. | y=-$\frac{1}{2}$(x-1)2+1 | D. | y=-$\frac{1}{2}$(x-1)2-1 |
7.下列调查中,适用采用全面调查(普查)方式的是( )
| A. | 对玉坎河水质情况的调查 | |
| B. | 对端午节期间市场上粽子质量情况的调查 | |
| C. | 对某班50名同学体重情况的调查 | |
| D. | 对为某类烟花爆竹燃放安全情况的调查 |
 如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )
如图,正方形ABCD的对角线BD长为2$\sqrt{2}$,若直线满足:(1)点D到直线的距离为1;(2)A、C两点到直线的距离相等,则符合题意的直线的条数为( )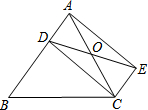 如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.
如图,已知D是△ABC的边AB上一点,CE∥AB,DE交AC于点O,且OA=OC.求证:四边形ADCE是平行四边形.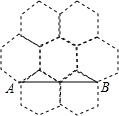 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.
蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有10.