题目内容
计算:
(1)(-12a2b2c)•(- abc2)2=______;
abc2)2=______;
(2)(3a2b-4ab2-5ab-1)•(-2ab2)=______.
解:(1)(-12a2b2c)•(- abc2)2,
abc2)2,
=(-12a2b2c)•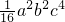 ,
,
=-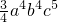 ;
;
故答案为:- a4b4c5;
a4b4c5;
(2)(3a2b-4ab2-5ab-1)•(-2ab2),
=3a2b•(-2ab2)-4ab2•(-2ab2)-5ab•(-2ab2)-1•(-2ab2),
=-6a3b3+8a2b4+10a2b3+2ab2.
故答案为:-6a3b3+8a2b4+10a2b3+2ab2.
分析:(1)先根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;单项式乘单项式,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式的法则计算;
(2)根据单项式乘多项式,先用单项式去乘多项式的每一项,再把所得的积相加的法则计算即可.
点评:本题考查了单项式与单项式相乘,单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意运算符号的处理.
 abc2)2,
abc2)2,=(-12a2b2c)•
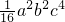 ,
,=-
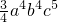 ;
;故答案为:-
 a4b4c5;
a4b4c5;(2)(3a2b-4ab2-5ab-1)•(-2ab2),
=3a2b•(-2ab2)-4ab2•(-2ab2)-5ab•(-2ab2)-1•(-2ab2),
=-6a3b3+8a2b4+10a2b3+2ab2.
故答案为:-6a3b3+8a2b4+10a2b3+2ab2.
分析:(1)先根据积的乘方,等于把积中的每一个因式分别乘方,再把所得的幂相乘;单项式乘单项式,把他们的系数,相同字母的幂分别相乘,其余字母连同他的指数不变,作为积的因式的法则计算;
(2)根据单项式乘多项式,先用单项式去乘多项式的每一项,再把所得的积相加的法则计算即可.
点评:本题考查了单项式与单项式相乘,单项式与多项式相乘,熟练掌握运算法则是解题的关键,计算时要注意运算符号的处理.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目