题目内容
(1)
-
+
(2)(
+
)(
-
)-(
-
)2-
(3)
-
•
(4)(-1)2009+3×(
)-1-|1-
|+(3.14-π)0.
| 18 |
| 72 |
| 50 |
(2)(
| 7 |
| 3 |
| 7 |
| 3 |
| 3 |
| 7 |
| 16 |
(3)
| ||||
|
|
| 6 |
(4)(-1)2009+3×(
| 3 |
| 3 |
考点:二次根式的混合运算,零指数幂,负整数指数幂
专题:计算题
分析:(1)先把各二次根式化为最简二次根式,然后合并即可;
(2)利用平方差公式和完全平方公式计算;
(3)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算;
(4)根据绝对值、零指数幂、负整数指数幂的意义得到原式=-1+3×
-
+1+1,然后进行二次根式的除法运算后合并即可.
(2)利用平方差公式和完全平方公式计算;
(3)先把各二次根式化为最简二次根式,然后进行二次根式的乘除运算;
(4)根据绝对值、零指数幂、负整数指数幂的意义得到原式=-1+3×
| 1 | ||
|
| 3 |
解答:解:(1)原式=3
-6
+5
=2
;
(2)原式=7-3-(3-2
+7)-4
=4-10+2
-4
=2
-10;
(3)原式=
-
=1-
;
(4)原式=-1+3×
-
+1+1
=-1+
-
+1+1
=1.
| 2 |
| 2 |
| 2 |
=2
| 2 |
(2)原式=7-3-(3-2
| 21 |
=4-10+2
| 21 |
=2
| 21 |
(3)原式=
2
| ||||
3
|
|
=1-
| 3 |
(4)原式=-1+3×
| 1 | ||
|
| 3 |
=-1+
| 3 |
| 3 |
=1.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂、负整数指数幂.

练习册系列答案
相关题目
用配方法解关于x的一元二次方程x2-2x-m=0,配方后得到的方程为( )
| A、(x-1)2=m-1 |
| B、(x-1)2=m+1 |
| C、(x-1)2=1-m |
| D、(x-1)2=m2-1 |
二次函数y=3(x+1)2+2的顶点坐标为( )
| A、(-1,-2) |
| B、(-1,2) |
| C、(1,-2) |
| D、(1,2) |
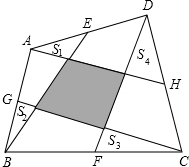 如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.
如图,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,图中阴影部分的面积为20平方厘米,求图中四个小三角形的面积和.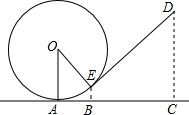 如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=
如图是小朋友玩的“滚铁环“游戏的示意图,⊙O向前滚动时,铁棒DE保持与OE垂直.⊙O与地面接触点为A.若⊙O的半径为25cm,cos∠AOE=