题目内容
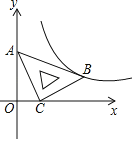
【题目】如图，已知平行四边形
中，
，
，
.平行四边形
的顶点
在线段
上（点
在
的左边），顶点
分别在线段
和
上.
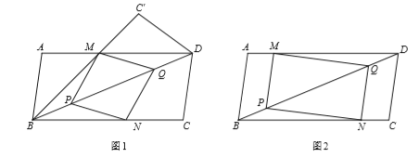
（1）求证：
；
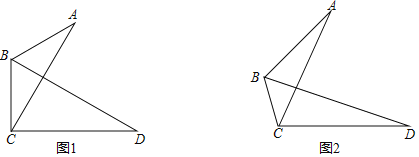
（2）如图1，将
沿直线折叠得到
，当
恰好经过点
时，求证：四边形是菱形；
（3）如图2，若四边形是矩形，且
，求
的长.（结果中的分母可保留根式）
【答案】（1）详见解析；（2）详见解析；（3）
【解析】
（1）根据平行四边形的性质可得
，从而得出
，再根据平行四边形的性质可得：
，
，从而得出
，即可得
，理由AAS即可证出
，从而得出
；
（2）根据折叠的性质可得
，根据（1）中的结论可得：
，再根据等角对等边可得
，从而得出
，理由SAS即可证出
，从而得出
，根据菱形的定义可得四边形
是菱形；
（3）过点
作
于点
，连接
交
于
.设
，根据矩形的性质和平行的性质可得
，
，然后用
分别表示出HQ、HN和BH，利用锐角三角函数即可求出x，从而求出
的长.
解：（1）如图，∵四边形
是平行四边形，
∴.
∴.
∵四边形是平行四边形，
∴，.
∴.
∴
在
和
中
∴.
∴.
（2）如图，∵
与
关于
对称，
∴.
由（1）得，
∴.
∴.
由（1）得，
∴.
∴.
由（1）得，
∴.
∵
，
在
和
中
∴.
∴.
∴
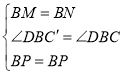
是菱形.
（3）如图，过点作于点，连接交于.设，
∵四边形
是矩形，
，
∴，，
∴
，
，
.
在
中，由
，得
，
解得
.
∴
.
练习册系列答案
小学课时特训系列答案
相关题目
