题目内容
11. 如图,A,B为某市中心的两座商场,分别在公路的两旁,由于人流量较大,经常堵塞,欲在公路上建一座立交桥PQ,缓解交通堵塞的情况,同时预防交通事故,则如何建立交桥PQ,使A到B的路程A→P→Q→B最短?要求立交桥PQ与公路垂直,并在图中画出路径.(公路两边a与b是平行的直线)
如图,A,B为某市中心的两座商场,分别在公路的两旁,由于人流量较大,经常堵塞,欲在公路上建一座立交桥PQ,缓解交通堵塞的情况,同时预防交通事故,则如何建立交桥PQ,使A到B的路程A→P→Q→B最短?要求立交桥PQ与公路垂直,并在图中画出路径.(公路两边a与b是平行的直线)
分析 将点A竖直向下平移到点A′,使AA′等于公路的宽度,连接A′B,与b交于点Q,过点Q作PQ⊥a于P,连接AP、BQ.则由A经过天桥走到B的最短路线的长:AP+PQ+QB=A′B+PQ.
解答  解:如图;①将点A竖直向下平移到点A′,使AA′等于公路的宽度,
解:如图;①将点A竖直向下平移到点A′,使AA′等于公路的宽度,
②连接A′B,与b交于点Q,
③过点Q作PQ⊥a于P,
④连接AP、BQ.
则天桥建在PQ处能使由A经过天桥走到B的路程最短,最短路线的长:AP+PQ+QB=A′B+PQ.
点评 本题主要考查了轴对称-最短路线问题,平行四边形的判定与性质,根据“两点之间,线段最短”找到桥址的位置是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
1.方程2-$\frac{2x-4}{3}$=-$\frac{x-7}{6}$去分母得( )
| A. | 2-2(2x-4)=-(x-7) | B. | 12-2(2x-4)=-x-7 | C. | 12-2(2x-4)=-(x-7) | D. | 以上答案均不对 |
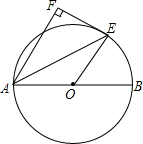 如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗?
如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗? 如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形.
如图,利用关于坐标轴对称的点的坐标特点,画出△ABC关于x轴或y轴对称的图形.