题目内容
直线l交y轴于点C，与双曲线
交于A、B两点，P是线段AB上的点（不与A、B重合），过点A、P、Q（Q在直线l上）分别向x轴作垂线，垂足分别为D、E、F，连接OA、OP、OQ，设△AOD的面积为S1，△POE的面积为S2，△QOF的面积为S3，则S1、S2、S3的大小关系为 ．（用“＜”连接）
【答案】分析：设PE与双曲线交于M点，延长FQ交双曲线与N点，连接MO，NO，则可以得到三个面积相等的三角形，再利用另外三个三角形与这三个三角形之间的关系即可比较出S1、S2、S3的大小关系．
解答：
解：如图：延长FQ交双曲线于N点，连接MO，NO，
∴S△ADO=S△MEO=S△NFO=S1，
由上图可知：S2＞S△MEO，S3＜S△NFO，
∴S2＞S1＞S3．
故答案为：S2＞S1＞S3．
点评：本题是一道反比例函数综合题，解题的关键是了解反比例函数上的一点向坐标轴作垂线，所构成的三角形的面积等于比例系数的绝对值的一半．
解答：
解：如图：延长FQ交双曲线于N点，连接MO，NO，∴S△ADO=S△MEO=S△NFO=S1，
由上图可知：S2＞S△MEO，S3＜S△NFO，
∴S2＞S1＞S3．
故答案为：S2＞S1＞S3．
点评：本题是一道反比例函数综合题，解题的关键是了解反比例函数上的一点向坐标轴作垂线，所构成的三角形的面积等于比例系数的绝对值的一半．
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
已知抛物线y=-x2+2mx-m2-m+2．
轴分别交于点C、D．直线EB交x轴于点F．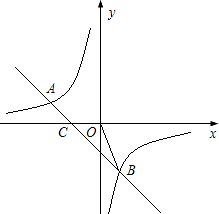
如图，一次函数y=kx+b的图象与反比例函数
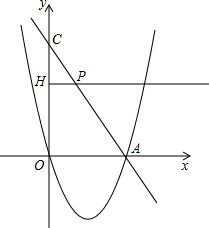如图，经过原点的抛物线y=x2-2mx与x轴的另一个交点为A．过点P（m+1，
如图，已知点D（6，1）是反比例函数